
Dr.Godfried-Willem RAES
Kursus Experimentele Muziek: Boekdeel
4: Akoestiek
Augent - : School of Arts
| <Terug naar inhoudstafel kursus> |
4040:
Snaren en hun berekening
Bazisgegevens:
Een snaar definieren we in de akoestiek en de organologie als een elastisch materiaal opgespannen tussen twee vaste punten. De verhouding lengte tot diameter moet zeer groot zijn en de oppervlakte van de doorsnede konstant over de gehele lengte. Het materiaal moet voorts homogeen zijn, maar kan zowel isotropisch als anisotropisch zijn. Last but not least, moet er ook een kracht op de snaar staan zo dat zij in rust strak staat (De rechte door het middelpunt van haar doorsnede moet evenwijdig zijn met de rechte tussen beide ophangpunten).
De grondfrekwentie waarmee zo'n snaar transversaal trilt wanneer we haar in het midden uit haar evenwicht brengen en weer loslaten, wordt gegeven door volgende formule, ook wel de wet van Taylor genaamd:

De spanning op de snaar -een kracht- wordt uitgedrukt in Newton, terwijl de densiteit hier overeenkomt met de massa van de snaar per meter (kg/m) . Het gedeelte onder de wortel bepaalt de snelheid waarmee een trilling zich langs de snaar voortplant (cfr. proef met de lange elastiek, waarmee we o.m. de fazeomkering bij het uiteinde demonstreerden). De lengte is de lengte tussen de twee vaste uiteinden en wordt uitgedrukt in meter. Merk op dat deze formule erg veel gelijkenis vertoont met die voor de berekening van de grondfrekwentie van aan beide zijden open buizen, waar we hadden:

(de luchtdruk van de omgeving is gewoonlijk 101000 Pascal terwijl de densiteit van lucht 1.20 kg/m3 is)
Aangezien de lengte in de noemer staat van de formule, volgt dat de toonhoogte stijgt naarmate we de lengte verkorten. Anders gesteld, de toonhoogte is omgekeerd evenredig met de lengte van de snaar.
Anderzijds blijkt ook uit de formule dat, voor een gelijke lengte, de toonhoogte zal stijgen naarmate we de spanning op de snaar vergroten. Deze spanning staat evenwel in de teller van de breuk onder de wortel. Dit betekent dat de toonhoogte niet lineair met de spanning toeneemt, maar omgekeerd kwadratisch. Dus, naarmate de spanning vergroot, wordt de toename van toonhoogte geringer. Dit kan uiteraard niet onbeperkt worden verdergezet, want vanzodra de snaarspanning de rekgrens van het materiaal te boven gaat, zal de snaar onder invloed van de kracht blijvend uitrekken -de toonhoogte stijgt niet verder- en beginnen vloeien wat uiteraard breken voor gevolg zal hebben. Het gebied waarvoor de samenhang tussen toonhoogte en snaarspanning geldig is wordt bepaald door de elasticiteitsmodulus van het materiaal. (zie tabel verder in dit hoofdstuk). De kracht waarbij breuk optreedt noemt men de breukgrens van de snaar.
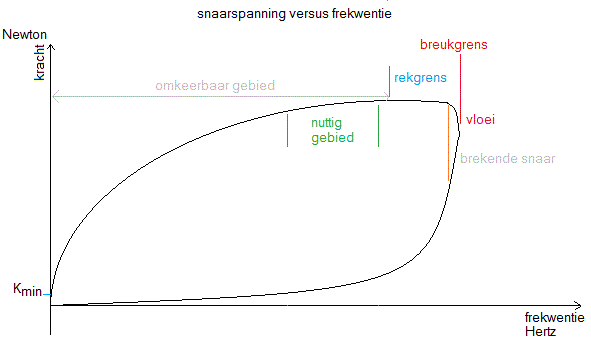
Tenslotte volgt uit het feit dat de densiteit van de snaar in de noemer staat van de breuk onder de wortel, dat de toonhoogte zal dalen naarmate we een dikkere snaar toepassen. Ook hier weer is het verband niet lineair. Uiteraard is er een strikt verband tussen de densiteit (overeenkomstig de dikte van de snaar en de massa van het materiaal waaruit ze is gemaakt) en de hoogste toelaatbare snaarspanning.
De spanning op de snaar is mede afhankelijk van de temperatuur. De snaarspanning neemt immers af met toenemende temperatuur, aangezien de snaar bij verwarming zal uitzetten. Omwille van het omgekeerde effekt (het toenemen van de snaarspanning bij dalende temperatuur), moeten de snaren van snaarinstrumenten die in het onverwarmd ruim van een eenvoudig vliegtuig worden getransporteerd (het kan er tot -50 graden celsius zijn!), steeds worden ontspannen. Zoniet riskeer je niet alleen snaarbreuk, maar ook een totaal gebarsten instrument...
Voor staal is de lineaire uitzettingskoefficient 0.000012 per graad. Voor messing in de orde van 0.0000185 per graad en voor inox ca. 0.000016 per graad. Voor een stalen snaar van 1 meter lengte betekent dit een lengteverandering van 0.6mm voor een temperatuursvariatie van 50 graden. Uiteraard kan de trillende lengte van een gespannen snaar niet veranderen, en derhalve zal die verandering zich tonen door een overeenkomstig veranderde kracht op de snaar.
De bovenstaande formule van Taylor laat ons toe de spanning op een snaar te berekenen wanneer we haar klinkende toonhoogte kennen en het gewicht per meter van het snaarmateriaal. Hierbij enkele waarden:
| materiaal | diameter | densiteit |
| staal | 1 mm | 0.0059 kg/m |
| staal | 0.5 mm | 0.0015 kg/m |
| darmsnaar | 0.6 mm | 0.0003 kg/m |
De midi-noot 60 Do in het midden van een piano kan bvb. een lengte hebben van 80 cm bij een snaardikte van 1 mm. Die noot komt overeen met een frekwentie van 262 Hz. Hieruit volgt, door toepassing van bovenstaande formule, dat op die snaar een spanning staat van 1030 Newton. Een gelijkaardige berekening voor een gitaarsnaar (hoge Mi-snaar): 65 cm lengte, 0.6 mm diameter, levert een kracht van 60 Newton. (We gaan uit van een diapason A = 440Hz).
De kracht op een snaar, K, kan ook worden berekend uit volgende formule, waarbij we uitgaan van de lengteverandering (delta L) die de snaar ondergaat onder invloed van de erop uitgeoefende kracht:
In deze formule is:
- Vrijheidsgraden: torsie, lengte (longitudinaal), dwars.
Merk op dat een trillende snaar niet in een vlak, maar in de ruimte beweegt. Anders gesteld, het trillingsvlak draait in de ruimte eliptisch om de as van de snaar. De omwentelingssnelheid van dit vlak is een torsie komponent van de trilling en hangt mee af van de excitatiewijze. In elk geval is de grondfrekwentie van de torsiekomponent heel veel lager dan de 'normale' grondtoon van de snaar. De torsiekomponent speelt een erg belangrijke rol bij strijkinstrumenten, waarbij de strijkstok immers een roterende trilling in de snaar veroorzaakt die interageert met de normale laterale trilwijze van de snaar.
- Trillingsvormen
Zoals we zien in de hieronder geherformuleerde formule, trilt een snaar in haar grondtoon als een halve golflengte. Verwar echter nooit deze golflengte van de trillende snaar met die van het erdoor voortgebrachte geluid! Bij snaren trilt het materiaal van de snaar, en geldt de voorplantingssnelheid van de trilling door dat materiaal voor de bepaling van de frekwentie. Deze trilling wordt (zij het voor een snaar zonder verdere hulpmiddelen, erg weinig) overgebracht door de omringende lucht, wanneer die aanwezig is. (Een snaar trilt immers ook in het luchtledige, al maakt ze dan wel geen geluid...).
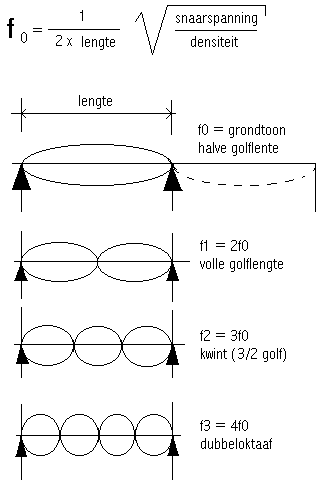
- Harmonischen en spektraalkomponenten
De 'harmonischen' reeks waarbij de meeklinkende boventonen uitsluitend bestaan uit gehele veelvouden van de grondtoon bestaat in de fysische werkelijkheid helemaal niet. Alleen in het rijk van Plato bestaat die, waar snaren immers gereduceerd worden tot lijnstukken, met een onbeperkte elasticiteit. In dat Platonische geval verhouden de harmonischen zich tot de grondfrekwentie als een reeks gehele getallen: 1,2,3,4,5,6,7,8,... (zie ook 1084.html, 1085.html en 1086.html)
Vanzodra een snaar een dikte heeft, ontstaat er een inharmoniciteit in de boventoonreeks, en zijn de 'harmonischen' niet langer een reeks gehele veelvouden van de grondfrekwentie, maar transcendente veelvouden van de grondfrekwentie. Wanneer we de dikte van de snaar laten toenemen tot we een ingeklemde staaf bekomen, dan hebben de spektraalkomponenten een kwadratisch verloop volgens de reeks 1, 4, 9, 16, 25, 36, 49...... De spektraalkomponenten van een werkelijke snaar liggen ergens tussenin beide reeksen. Naarmate de elasticiteit van het snaarmateriaal kleiner is, wordt de trilling ervan minder uitsluitend bepaald door de mate waarin we haar exciteren en meer door de eigen veerkracht (de stijfheid) van het materiaal. In dit geval zullen de boventonen allemaal wat groter zijn dat de reeks gehele getallen.
De benaderingsformule die ons toelaat de frekwentie van de boventonen van een werkelijke snaar te berekenen ziet eruit alsvolgt:
f(n) = n * f(0) * SQR(1 + (B*(n^2)))
waarin:
waarin dan weer:
Het is duidelijk dat wanneer d = 0, het resultaat van B eveneens nul wordt, waardoor de formule tot zijn platonische vorm f(n) = n* f(o) wordt teruggebracht. Ook duidelijk moet zijn -en dat is een spektakulair resultaat- dat het spektrum, en daarmee het timbre ervan- een funktie wordt van de toon waarop de snaar wordt gestemd! Elke violist weet dat zonder het echt te weten... Hij meent veelal over een absoluut gehoor te beschikken (wat niet kan) terwijl hij in werkelijkheid een goed geheugen heeft voor klankkleuren, wat we allemaal min of meer goed kunnen. Immers zoniet zouden we nooit iemand aan zijn stem kunnen herkennen. De getrainde violist herkent de 'goede' stemming van zijn instrument aan de hand van de specifieke kleur.
De oorzaak van dit verschijnsel bij snaren is volkomen analoog aan wat we stelden bij de behandeling van pijpen en luchtkolommen: daar goldt dat de eindkorrektie eveneens een funktie is van het volgnummer van de boventoon. Bovendien is de toonhoogte en het gehele spektrum daar ook een funktie van de winddruk waarmee de pijp wordt aangeblazen. Bij snaren ligt de oorzaak enerzijds in het feit dat de propagatiesnelheid van trillingen in het materiaal een funktie is van de frekwentie van de trilling, anderzijds dat ook hier de feitelijk trillende lengte verschillend is (korter) naargelang de boventoon hoger is.
Ook elke afwijking van materiaalkonsistentie en dikte in het verloop van de snaar, heeft inharmoniciteit voor gevolg. Deze parameters werden weggelaten uit bovenstaande formule, evenals de torsiekomponent, de longitudinale komponent en de amplitude variatie in de tijd. Ook wordt uitgegaan van een vrij trillende snaar, dus niet een met een strijkstrok, plektrum, hamer... aangedreven snaar tijdens de aandrijving.
Precieze metingen uitgevoerd op een goede nylon sol-snaar van een gitaar, leverden bvb. volgend rezultaat op voor de verhouding van boventonen tot de grondtoon:
| grondtoon | 'oktaaf' harmoniek | 'kwint' harmoniek | 'dubbeloktaaf' harmoniek | 'terts'harmoniek |
| 1.000 | 2.007 | 3.009 | 4.015 | 5.015 |
De gemeten waarden hangen in sterke mate af van de stemming van de snaar. Voor een stalen snaar, met een grotere stijfheid, is die inharmoniciteit vele malen groter. Een volledig berekend en uitgewerkt voorbeeld, voor zo'n pianosnaar namen we op onder 1086.html.
Hoewel de termen 'harmonischen' of harmonieken en boventonen in het nederlands gangbaar zijn, kan worden getwijfeld aan hun geschiktheid om de hier behandelde verschijnselen te beschrijven. Vooreerst, zoals bleek, zijn die harmonischen helemaal niet zo 'harmonisch'. Verder zijn er naast 'boventonen' in trillende snaren (maar meer nog in membranen en tongen) ook 'ondertonen'. Het engelse begrip 'partial' brengt dit beter tot uitdrukking, omdat elke willekeurige spektraallijn ermee kan worden aangeduid. We zouden hiervoor de nederlandse term 'deeltonen' kunnen hanteren, maar erg gebruikelijk is dit niet. 'Spektraalkomponenten' klinkt wat ingewikkelder, maar drukt de fysische achtergrond goed uit.
- Excitatie vormen
Een snaar trilt niet vanzelf. Om ze tot trilling te brengen moet er een kracht op worden uitgeoefend en wel zo dat ze uit haar evenwicht wordt gebracht. Het voortgebrachte spektrum is bij snaren heel erg afhankelijk van de plaats waar de snaar wordt geexciteerd. Op de plaats van excitatie kan immers in het trillingpatroon en bij het begin van de excitatie, geen knoop bestaan, maar slechts een buik. De boventoon die op die plaats een knoop heeft, zal dan ook sterk worden onderdrukt.
Wanneer een snaar in het midden wordt aangeslagen of getokkeld, dan heeft het klinkend spektrum geen even boventonen, aangezien die allemaal een knoop moeten hebben in het midden van de snaar. Wanneer we een snaar op 1/6e van haar lengte aantokkelen, zoals afgebeeld in onderstaande tekening waarin het excitatiepunt is aangegeven met een rode pijl, dan krijgen we een sterke onderdrukking van de zesvoudige grondfrekwentie en een sterke benadrukking van de drievoudige grondfrekwentie, in dit geval dus de kwint. Wanneer we evenwel op een van de punten 1/3L of 2/3L tokkelen, zullen we daareentegen precies de kwint onderdrukken.

Algemeen, wanneer we een snaar op 1/N e van haar lengte aantokkelen, dan zullen
alle spektraalkomponenten die overeenkomen met de N-de boventoon en de veelvouden
daarvan worden onderdrukt. Dit gegeven wordt in instrumentenbouw positief gebruikt
om bepaalde (in)harmonischen in het spektrum van een trillende snaar te bevoordelen:
we slaan de snaar aan op die plek waar de gewenste (in)harmonische een buik
moet hebben en de ongewenste een knoop. In de in de westerse muziek dominante
gelijkzwevende 12-toons stemming, is de 7e boventoon (de kleine septiem) te
laag. Om die toon te onderdrukken, kunnen we de snaren in een instrument dan
ook bij voorkeur aanslaan op 1/7e van hun lengte. Op 1/9e van de lengte zullen
we de eveneens 'niet in het systeem passende' sekonde, dempen.
Excitatiewijzen:
Dat de manier waarop en de plaats waar een snaar wordt geexciteerd een bepalende invloed heeft op het voortgebrachte spektrum weten ook alle violisten welhaast intuitief: ze kennen goed het verschil tussen 'sul tasto' en 'sul ponticello': hoe meer sul tasto wordt gespeeld, hoe doffer het geluid, terwijl naar de kam toe een alsmaar schrieler geluid kan worden geproduceerd.
In getokkelde en aangeslagen toetsinstrumenten is de plaats van aanslag een konstante in het ontwerp van het instrument. Voor pianos ligt het aanslagpunt -het punt waarop de hamer de snaar raakt- tussen 1/8 en 1/10 van de snaarlengte. Hoe kleiner het raakvlak tussen snaar en hamer, hoe scherper de toon zal zijn. Uiteraard ook, wanneer de hardheid van de hamer groter wordt. De oppervlakte waarmee de vilten hamers van een piano de snaar raken is dan ook bepalend voor de voortgebrachte toon. Ook de densiteit van het gebruikte vilt speelt een belangrijke rol, want hiervan hangt het af hoe lang de hamer kontakt maakt met de snaar. Hoe harder het vilt, hoe veerkachtiger de botsing met de snaar en ook hoe minder boventonen zullen worden onderdrukt. Versleten en verhard vilt op de hamerkoppen van een piano doen deze dan ook metaliek klinken. (Honky tonk piano).
Breukgrenzen voor gebruikelijke stalen snaren (piano snaar, fabrikaat Moritz Poehlmann), rezultaat van experimentele metingen:
| Diameter in mm | nummer (US/Brit) 'standard wire gauge' | breukgrens | |
| 0.76 |
13 (dit is de kleinste diameter gebruikt in de pianobouw) |
163 kgf = 1599 N | |
| 0.79 | 14 | 168 kgf = 1648 N | |
| 0.81 | 15 | 175 kgf = 1717 N | |
| 0.89 | 16 | 200 kgf = 1962 N | |
| 0.94 | 17 | 208 kgf = 2040 N | |
| 1.02 | 18 | ||
| 1.07 | 19 | ||
| 1.12 | 20 |
Modernere snaren -bvb. zoals gemaakt door de firma Bekaert bij ons- kunnen veel hogere breukgrenzen hebben en kunnen dan ook worden toegepast onder hogere spanningen. Het gebruik van stalen snaren is in de loop van vorige eeuw ook ingeburgerd geraakt op strijkinstrumenten (de mi snaar op de viool o.m.) en zelfs op tokkelinstrumenten (elektrische gitaar, folkgitaar, banjo, mandoline...). Bij de elektrische gitaar is dit natuurlijk gedikteerd door de noodzakelijkheid een magnetiseerbaar materiaal te hebben (ijzer, cobalt of nikkel bvb.) aangezien het werkingsprincipe van de opneemelementen hierop berust.
Dimensionering van snaarlengtes en diameters in toetsinstrumenten:
Het teoretisch uitgangspunt bij het berekenen van de besnaring voor toetsinstrumenten zoals de pianoforte bestaat erin de kracht op elke snaar zoveel mogelijk gelijk te houden en de lengte aan te passen aan de voort te brengen toonhoogte. Zouden we dit strikt toepassen, dan zou de laagste C (midi noot 24) op het pianoklavier een snaar moeten aanslaan met een lengte van 6.50 meter, terwijl de hoogste C -snaar slechts 5cm lang moet zijn. Dergelijke piano zou dan ook circa 7 meter lang worden.
Om dit soort problemen te vermijden, worden de lage snaren in pianos korter gedimensioneerd terwijl hun massa wordt vergroot door omwikkeling met koperdraad. Puur teoretisch gezien, zouden Osmium (22,59 g/cm3), Iridium (22.56 g/cm3), Wolfram, Platina of... verarmd uranium een ideaal materiaal moeten zijn voor dit doel: immers de massa is twee tot viermaal zo groot dan die van koper, zodat de diameter van de snaren veel minder zou moeten aangroeien met dalende toonhoogte. Wanneer je weet dat bvb. Iridium ongeveer tienmaal zoveel kost dan platina, zal je begrijpen dat zulke snaren niet worden gemaakt... (Cfr. 4450.html voor een tabel met materialen)
Een door pianobouwers (ontwerpers, niet namakers en nabouwers...) gebruikte formule voor het inschalen van de lengtes van de niet omwikkelde snaren in een piano of pianoforte:
Log(Snaarlengte (noot)) = (0.025086 * (refnoot - noot) ) + Log(Snaarlengte(refnoot))
De zo bekomen reeks snaarlengtes wordt beschouwd als het ideaal vertrekpunt voor de dimensionering ('mensurering' in het instrumentenbouwers jargon) van het instrument. Wanneer daar, omwille van een kompaktere bouw van het instrument, moet worden van afgeweken, verkort men deze lengtes en vergroot men de diameter van de staaldraad proportioneel. Zo wordt de diameter van de pianosnaren in kleine vleugelpianos en buffetpianos vaak om de vijf halve tonen, een stapje groter genomen. De kracht op elke snaar wordt daarbij zoveel mogelijk gehouden op 785 N (80kgf), en zal in de praktijk zelden de helft van de breukgrens overschrijden. De dikte van de laagste niet omwikkelde snaar korrespondeert meestal met nummer 24 uit de Brits-Amerikaanse standaard reeks, helaas nog steeds in gebruik in de toch wat retardaire sektor van de instrumentenbouw.
Rond midi noot 48 -de exakte noot hangt af van het formaat van de piano en van de bouwer- beginnen verder gaand naar de bas, de omwikkelde snaren. De kerndraad van de hoogste omwikkelde snaar is heel wat dunner dan de diameter van de eerste erboven liggende niet omwikkelde snaar. (meestal nummer 17 of 18). Dat is gedaan om zoveel mogelijk de timbrale diskontinuiteit die dergelijke overgang inherent met zich moet brengen, zoveel mogelijk te maskeren. Bovendien wordt de eerste omwikkelde snaar circa 1/6 korter genomen dan de eerst hogere niet omwikkelde snaar.
Timbre
Zoals hiervoor reeds gezegd, zal de klankkleur van de toon voortgebracht door een snaar afhangen van de wijze waarop en de plaats waar we die snaar tot trillen brengen. Maar, ook het materiaal waaruit de snaar is samengesteld is bepalend voor een flink deel van het voortgebrachte spektrum. Vooral de eigenschappen hardheid en elasticiteit spelen daarin een belangrijke rol. Van de voor snaren gebruikelijke materialen is staal wellicht het hardste materiaal. Hoe harder het materiaal hoe meer hoge komponenten het spektrum zal kunnen bevatten. Messingsnaren klinken dan ook 'ronder' dan staalsnaren. Nylon of darmsnaren hebben een geringe hardheid, maar een erg grote elasticiteit. De elasticiteit van een snaar is bovendien niet konstant. Een gespannen snaar verliest beetje bij beetje iets van haar elasticiteit en gaat dan ook na verloop van tijd makkelijker breken. Technisch noemt men dat materiaalmoeheid. De molekulaire struktuur (het kristalrooster) van het materiaal raakt verbroken waardoor de snaar niet langer als homogeen kan worden beschouwd. Dat zo'n snaar ook anders gaat klinken wanneer materiaalmoeheid begint op te treden, is iets waarmee violisten en gitaristen wel vertrouwd zullen zijn.
Dat het spektrum van een snaar een funktie is van de materiaaleigenschappen bleek al uit de hoger gegeven formules. De parameters voor de elasticiteitsmodulus en de propagatiesnelheid van trillingen in diverse materialen behandelen we in 4450.html
Gespannen snaren, analytisch bekeken...
In onderstaande figuur hebben we een snaar gespannen tussen twee vaste punten (bruggen) getekend.
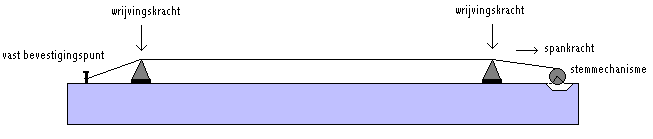
De door het stemmechanisme (meestal een cilindrische trommel) op de snaar gebrachte kracht is de som van de kracht op het trillend gedeelte van de snaar, de kracht veroorzaakt door de hoek die de snaar maakt over de bruggen en de twee wrijvingskrachten die werken tussen snaar en brug. Deze laatste krachten zijn de oorzaak van de hysteresisch waarmee we steeds te maken hebben wanneer we een snaar met het mechanisme willen stemmen. De kracht die ontstaat doordat de snaar een hoek vormt met de bruggen, zorgt ervoor dat de trilling via die bruggen op de klankkast kan worden overgebracht. Hoe scherper die hoek, hoe groter de aandrukkracht zal zijn. Wanneer die aandrukkracht groter is, stijgt ook de intensiteit van de trilling die kan worden overgebracht. Dit is ook de reden waarom men in het begin van de 19e eeuw alle strijkinstrumenten (Stadivarius, Guarneri etc...) is gaan ombouwen zo dat de toets een scherpere hoek vormde met de klankkast. Aan dit vergroten van de hoek is echter ook een nadeel verbonden: immers ook de wrijving van de snaar op de brug neemt erdoor toe, wat het stemmen alleszins niet makkelijker maakt en ook het risiko op snaarbreuk evenredig doet toenemen.
De formule voor de berekening van de toonhoogte van een snaar zoals hierboven gegeven is korrekt, maar maakt abstraktie van zowel de wrijvingskrachten als de aandrukkrachten op de brug zelf. De in de praktijk door het stemmechanisme te bewerkstelligen kracht is dan ook steeds groter dan de snaarspanning strictu sensu.
De stijfheid van een snaar heeft niet alleen een zekere mate van inharmoniciteit voor gevolg die ontstaat op de beide kammen waartussen de snaar is gespannen, maar evenzeer voor de klankkleur die ze voortbrengt wanneer ze met een hard voorwerp (plektrum, vingernagel...) wordt getokkeld.
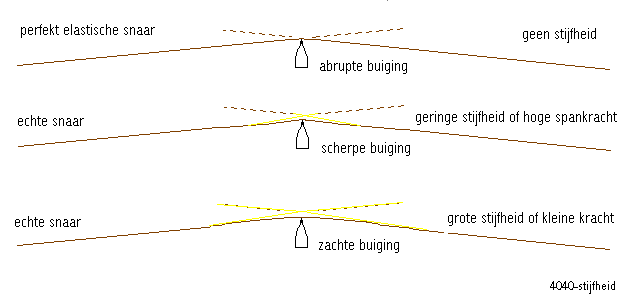
Zoals blijkt uit de tekening, wordt de buighoek gevormd door snaar en objekt bepaald door zowel de eigen stijfheid van de snaar als door de kracht die eop wordt uitgeoefend. Wanneer snaren veschillende diameters hebben, zijn ook hun buiginghoeken, bij gelijke spankracht, verschillend. Onder meer hierdoor zouden de fretten op een gitaar voor elke snaar iets anders moeten staan. (zie ook 4046.html).
Naarmate de buiging van een snaar zachter is (onderste tekening) worden hogere boventonen meer onderdrukt. Bij een scherpe buigingshoek, is de toon heel wat briljanter. Dat een piano 'ronder' klinkt dan een klavecimbel, is onder meer te wijten aan de veel grotere stijfheid van de stalen pianosnaren in vergelijking van de messingsnaren op een klavecimbel. Ook de ronde vorm van de vilten hamers strekt er natuurlijk toe de grondtonigheid van de voortgebrachte klank te bevorderen.
Zoals eerder reeds gezegd, heeft, naast de plek van excitatie, ook de excitatiewijze van een snaar een bepalende invloed op het voortgebrachte spektrum. Voor getokkelde instrumenten vormen de amplitudes van de boventonen een benaderende reeks van de vorm:
1/1^2 , 1/2^2, 1/3^2, 1/4^2, 1/5^2 enz... 1/n^2
Voor een met een gewogen hamer aangeslagen snaar (piano) evenwel geldt de benaderende reeks:
1, 1/2, 1/3, 1/4, 1/5, 1/6 ... enz.. 1/n
Voor een gestreken snaar is de zaak heel wat komplexer (cfr. 4041.html).
Uiteraard moeten deze principes toegepast worden in kombinatie met wat we zegden over de plaats van aanslaan of tokkelen , het slagmateriaal e.d.m.
Ongewilde afwijkingen
- gevolgen van onregelmatigheden in het dikteverloop van snaren
- gevolgen van torsie op snaren
- terugkoppeling van de frame- en klankkast resonanties op de trilling van de snaar zelf
- onderlinge beinvloeding van de snaren.
Gewilde afwijkingen en preparaties
- Prepared piano
- Prepared guitar...
Golfvergelijking
Voor wie zich wiskundig voldoende onderlegd voelt, geven we hier graag ook een link naar een bijzonder mooi bewijs voor de vereenvoudigde golfvergelijking van een trillende snaar: http://www.math.ubc.ca/~feldman/apps/wave.pdf
Mocht de link niet goed werken, hier is een alternatief.
Verdere lektuur:
ROSSING, Thomas.D (editor), "The Science of String Instruments"
Filedate: 970928/ updated 2013-06-21
| Terug naar inhoudstafel kursus: <Index Kursus> | Naar homepage dr.Godfried-Willem RAES | bibliografie en verdere lektuur |