Dr.Godfried-Willem RAES
Kursus Akoestiek
Hogent: School of Arts
| naar inhoudstafel akoestiek |
Hoe geluid - een trillingsverschijnsel - zich voortplant door
gassen en gasmengsels zoals lucht er een is, zagen we reeds in de eerste paragrafen
van deze kursusnotas. Trillingen in vloeistoffen en vaste stoffen -zelfs
wanneer ze naar frekwentie binnen het audio-bereik zouden vallen- zijn bij definitie
geen geluiden. Wel zijn ze in heel veel gevallen de oorzaak van geluiden, omdat
hun trillend oppervlak in kontakt staat met de omgevende lucht op dewelke de
trillingen worden overgedragen. Een tollende klok met klepel op de maan trilt
op de maan weliswaar minstens net zoveel en op dezelfde wijze als op aarde,
maar zal op de maan geen enkel geluid kunnen voortbrengen: er is immers geen
lucht. Hoe groter het kontaktoppervlak van de trillende substantie met de omgevende
lucht, hoe meer lucht in trilling kan komen. Het totale akoestische vermogen
dat vanuit het trillend medium op de lucht wordt overgedragen neemt dan ook
evenredig toe met het oppervlak van dat medium. Uiteraard moeten we hier de
wet van behoud van energie in acht nemen, waardoor in elk geval de totale afgestraalde
energie nooit groter kan zijn dan de energie van de trilling van de vaste stof
zelf. Het vergroten van het kontaktoppervlak leidt dan ook slechts tot een grotere
afgestraalde akoestische energie, wanneer die energie ook door de bron kan worden
geleverd. Hieruit mogen we echter niet meteen besluiten dat een groter trillend
oppervlak zelfs in acht genomen deze beperking, ook automatisch een luider geluid
oplevert. Immers, het fenomeen kan zich voordoen dat voor bepaalde frekwenties
de trilling in tegenfaze wordt afgestraald, waardoor de amplitude op een bepaald
punt van waarneming verzwakt. Ook het omgekeerde verschijnsel kan zich trouwens
voordoen. De geluidsdruk op een bepaald waarnemingpunt in de ruimte hangt af
van de koordinaten van dat punt tegenover die van de trillende substantie en
uiteraard van de afstand tot die bron. Dit verschijnsel ligt ten andere ten
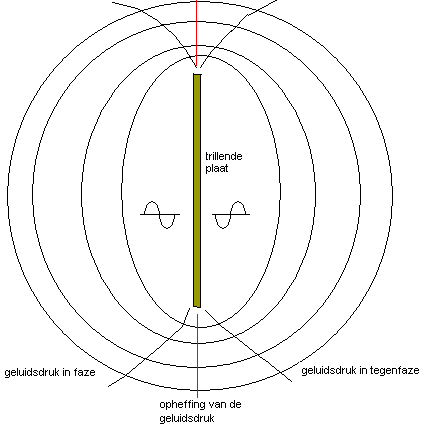
grondslag aan het steeds in een behuizing (gesloten kast) inbouwen van luidsprekers.
Zonder zo'n kast zouden de door de achterzijde van de konus afgestraalde trillingen
deze afgestraald door de voorzijde ervan (althans voor lage frekwenties waarvan
de golflengte groter is dan de diameter van de luidspreker) , opheffen aangezien
zij in tegenfaze zijn. Met een losse niet ingebouwde luidspreker kunnen we dan
ook nooit een voortreffelijke basweergave verkrijgen. We hebben gepoogd dit
in volgende tekening te illustreren:

De snelheid waarmee een trilling (een elastische kleine beweging rond een statisch evenwicht in die stof) zich binnen een stof voortplant is een funktie van een aantal fysische eigenschappen van die stof: de densiteit, de elasticiteit en de struktuur die homogeen of niet homogeen kan zijn. We noemen een stof homogeen wanneer de voortplantingssnelheid van een trilling in die stof onafhankelijk is van de richting. Vloeistoffen zijn bijna altijd homogeen wanneer we ze in relatief kleine hoeveelheden beschouwen en voorzover ze in rust zijn (d.w.z. niet stromen noch turbulent zijn). Voor oceanen en zeeen gaat dat evenwel niet op (zie voetnoot). De meeste metalen en metaallegeringen kunnen we eveneens als homogeen beschouwen. Het gebeurlijk niet homogeen zijn van metalen (bvb. in lasnaden of gietstukken) wordt gezien als een fabrikagefout, een fout die trouwens veelal via akoestisch ultrasoononderzoek aan het licht wordt gebracht. Natuurlijke grondstoffen van organische oorsprong zijn bijna nooit homogeen: hout bvb. In hout is de voortplantingssnelheid van trillingen in de vezelrichting zowat het drievoudige van die gemeten loodrecht op de vezels. De juiste verhouding is evenwel geenszins konstant en hangt sterk af van de houtsoort, de wijze waarop het hout werd versneden, de groeisnelheid en eventueel toegepaste houtverbeteringstechnieken (minerale, synthetische of organische drenkstoffen of zogenaamde porienvullers).
Voor homogene materialen is de voortplantingssnelheid van trillingen steeds v = SQR(q/rho), waarin q= Young modulus (of elasticiteitsmodulus) in Pa en rho = densiteit van het materiaal in kg/m^3. Voor metalen zoals staal (elasticiteitsmodulus ca. 2E11 en massa ca. 7.3kg/dm3) ligt deze snelheid op ongeveer 5200m/s, voor vloeistoffen zoals water tussen 1450m/s en 1570m/s, afhankelijk van de samenstelling. Aangezien geen enkel ons bekend muziekinstrument gebruik maakt van trillingen die hun oorsprong vinden in vloeistoffen, kunnen we de behandeling daarvan hier verder rustig buiten beschouwing laten. Wie zich wil toeleggen op geluiden van dolfijnen en vissen, ultrasone echolokatie onder water enzomeer laten we dus op zijn honger. Dat in vaste stoffen de voortplantingssnelheid van trillingen heel wat groter is dan in lucht toonden we eerder in deze kursus aan met behulp van de proef met de knikkerbaan. Bij vaste stoffen liggen de molekulen waaruit ze is opgebouwd zonder tussenruimte tegeneen en kunnen ze al evenmin vrij over elkaar bewegen zoals ze dat wel kunnen in vloeistoffen. Hoe groter de hardheid van de stof, hoe hoger ook de snelheid waarmee een trilling zich erdoor zal kunnen voortplanten. Aan het einde van deze paragraaf voegden we een tabel toe met de voor de trillingsleer belangrijke eigenschappen van enkele vaak gebruikte materialen.
De voortplantingssnelheid van een trilling door vaste stoffen is van groot belang voor de berekening van de toonhoogte van gespannen snaren, (cfr. de behandeling van snaren in paragraaf 4040), maar is ook tengrondslagliggend voor de berekening van trillende staven (vibrafoons, glockenspiel, celesta), cimbalen, klokken en gongs. Hier hebben we telkens te maken met homogene stoffen. De meeste van deze homogene stoffen zijn ook isotropisch, d.w.z. hun fysische eigenschappen zijn gelijk in alle richtingen. Er zijn ook homogene stoffen (vele ferriet samenstellingen, kwarts, mica... bvb.) die anisotropisch zijn. Dit hangt samen met de kristallijne struktuur van die stoffen. Ook het koud vervormen van metalen zoals staal en roestvast staal maakt het materiaal anisotropisch. Niet homogene stoffen kunnen zowel isotropisch (bvb. beton, papier, ...) als anisotropisch (bvb. hout, sommige glasvezelversterkte epoxyharsen,...) zijn. In hout wordt de anisotropie veroorzaakt door de afwisseling van harde vezels met zachte cellulose vulstof.
Niet homogene en anisotropische stoffen, inzonderheid hout, zijn traditioneel bijzonder populair gebleken in de westerse instrumentenbouw tradities. Hout wordt niet alleen rechstreeks gebruikt als klankbron in instrumenten zoals de marimbafoon, xylofoon, woodblock, templeblock, claves, log drum... maar ook als klankblad in snaarinstrumenten zoals de vioolfamilie, klavecimbel, klavichord, piano, harp, hurdy gurdy, gitaar, crwth, koto, luit, vedel, gamba... De voortplantingssnelheid van trillingen in hout bestaan in hoofdzaak uit twee komponenten:
Een derde komponent, Vl, de longitudinale voortplantingssnelheid van trillingen door hout speelt in de praktijk nauwelijks een rol. We zouden het hooguit kunnen ontmoeten wanneer we hout kops zouden gebruiken als element in een systeem van trillingsoverdracht (dat is het geval voor de ziel van een viool), of wanneer we hout zouden gebruiken als snaarmateriaal... (Merk op: dit idee is niet zo gek als het klinkt, want in vele muziekkulturen van het verre oosten bestaan inderdaad zithers met snaren uit gespannen bamboevezels!)
Het verschil tussen beide propagatiesnelheden kan gemakkelijk worden duidelijk gemaakt met een stuk onbeplakt golfkarton: wanneer we het over en weer schudden evenwijdig met de golfjes dan zien we een golf ontstaan met een zichtbaar lage frekwentie. Keren we het karton nu negentig graden, dan zouden we al heel veel sneller moeten schudden om het karton in resonantie te krijgen.
De absolute waarde van Vd neemt af naarmate het hout verder uiteen liggende nerven heeft. De ruimte tussen de nerven is dan opgevuld met meer van de minder gebonden celstof. Ook zal de demping van de trilling groter zijn naarmate de nerven verder uiteen liggen en met zachtere celstof zijn opgevuld.
Voor hout is de verhouding Vv / Vd ongeveer gelijk aan 3. De juiste verhouding is zeer sterk afhankelijk van de houtsoort en ook verschillend voor elk individueel stuk hout. Een goede instrumentenbouwer moet dan ook in staat zijn dit voor elk gegeven stuk hout zelf te evalueren. Daarom behandelen we hier een praktische proef die een opmeting van beide propagatiesnelheden toelaat.
1. Proefopstelling voor het meten van de propagatiesnelheid van trillingen in vaste stoffen. Labo-versie.
nodige toestellen:
Voor de konstruktie van het opneemelement is wat knutselwerk nodig: ga uit van een piezo-schijfje van 12 tot 30mm doorsnede en soldeer daarop op lage temperatuur en aan de messingkant een verkoperde of vernikkelde duimspijker (punaise). Desnoods kan je ook epoxylijm gebruiken, maar wat soldeerervaring heb je in het beroep van instrumentenbouwer, producer en eigentijds komponist sowieso nodig... Soldeer aan de messingrand de afscherming van een eind afgeschermde mikrofoonkabel en (heel snel en voorzichtig...) aan de met een opgedampt zilverlaagje bedekte keramische kant, het uiterste puntje van de binnengeleider.
Test het geheel en wanneer het nog steeds een signaal afgeeft, kan je de keramische kant bedekken met een laagje zuurvrije siliconenrubber. Laat 24uur verharden voor verder gebruik.
Het elektromagnetisch kloppertje kunnen we ook eenvoudig zelf maken met een elektromagneet voorzien van een weekijzeren kern, waarin we een klein staafje (of een kopspeld met een ultradikke kop) monteren. (gaatje boren en staafje of naald inlijmen met cyaanacrylaat lijm).
De sturing van de elektromagnetische klopper kan met een enkele mosfet en een beveiligingsdiode (om de induktiestoot op te vangen) opgebouwd worden:
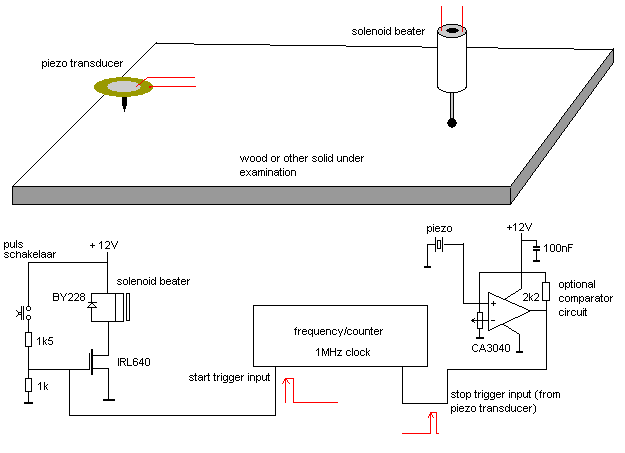
De schakeling en opstelling werkt wanneer we de schakelaar kort indrukken: het kloppertje tikt tegen het materiaal en de chrono wordt gestart. Wanneer de piezo de eerste puls ontvangt (eventueel moet een voorversterker of een komparatorschakeling -hierboven getekend- toegepast worden, afhankelijk van de instelmogelijkheden voor de gevoeligheid van de gebruikte counter), stopt de counter. Triggering moet gebeuren op de stijgende flank van het signaal. Op het display lezen we onmiddelijk de tijd in microsekonden af die de puls nodig had om zich van het kloppertje naar de piezo voort te planten. Wanneer we nu de afstand tussen beide punten precies meten met de schuifpasser, is de voortplantingssnelheid in die richting heel eenvoudig te berekenen. (v = s/ t)
In deze opstelling schuilt nog een foutje dat we makkelijk kunnen verhelpen: de magnetisering van de kern van het spoeltje en de versnelling van die kern tot op het moment dat het voorwerp geraakt wordt neemt ook een zekere tijd in beslag (0.1 tot 15ms). Deze tijd kunnen we opmeten door het kloppertje met dezelfde opstelling op de piezo te laten tikken en die tijd op te meten. Die kunnen we dan aftrekken van de eigenlijke tijd uitgelezen met de eerder beschreven proef. Natuurlijk kan je ook twee piezo's gebruiken: een voor start en een voor stop.
2. Opstelling onder gebruikmaking van een PC voorzien van een geluidskaart en een stereo ingang.
nodige software:
- WaveLab, Sonar, Soundscape, Cooledit, GMT, of eender welk ander PC programma dat toelaat signalen in het audiogebied per afzonderlijk sample te bekijken op het schern.
nodige hardware:
De opstelling ziet eruit alsvolgt:

Werkwijze:
Prik de piezotransducers op een met de schuifpasser bepaalde gelijke afstand van een punt op het houtoppervlak zo dat beide assen een rechte hoek vormen en bovendien een van beide assen evenwijdig loopt met de vezelrichting van het hout. Markeer het referentiepunt want dit wordt de plek waar we middels de stemvork een trilling doorheen het stuk hout gaan sturen. Start het programma op de PC op voor klankopname naar disk. Sla de stemvork aan en druk ze zo precies mogelijk op het gemarkeerde punt. Wanneer de stemvork is uitgetrild stop je de opname.
Bekijk de opgeslagen golfvormen in het scherm en ga na hoeveel samples er tussen beide opnamekanalen geteld kunnen worden. Bij een bemonsteringssnelheid van 44.1kS/s duurt 1 sample 22.675µs. Hieruit kan je de verhouding van de propagatiesnelheid in vezelrichting en tegen de vezelrichting bepalen. De bepaling van de absolute propagatiesnelheid is bij deze opstelling nauwelijks met wetenschappelijke precizie uit te voeren, want we kunnen niet de stemvork en een van de transducers op eenzelfde punt aanbrengen. Een idee van de grootte orde van de propagatiesnelheid kan dit wel opleveren.
Betekenis voor de instrumentenbouw:
Talloze instrumenten uit onze muzikale geschiedenis maken gebruik van een houten klankblad: de bovenbladen van alle instrumenten uit de strijkersfamilie, de harp, de piano net zoals overigens alle besnaarde toetsinstrumenten, klassieke gitaren, mandolines, luiten, zithers... Geen enkele historische instrumentenbouwer was zich bewust van hetgeen we hiervoor m.b.t. propagatiesnelheden van trillingen schreven. Hun kunde steunde enerzijds op pure traditie en anderzijds op wetenschappelijk niet onderbouwde ervaring. Niettemin blijkt uit hun resultaten dat de hierboven verklaarde verschijnselen toch hun weerslag hebben weten te vinden op de praktijk van de instrumentenbouw. Hoe anders kunnen we de als optimaal beschouwde lengte - breedte verhoudingen van de klankkasten (en bovenbladen) van viool, altviool, cello en kontrabas verklaren. Die verhoudingen komen wonderwel overeen met de verhouding van propagatiesnelheden in gemiddelde in instrumentenbouw gebruikelijke houtsoorten.
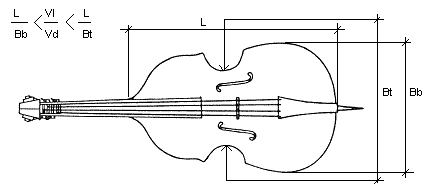
Precies omwille van die ongelijke verhoudingen zou het onzin zijn een viool te willen bouwen met een ronde klankkast. Daareentegen, gesteld dat we een viool zouden willen bouwen gebruik makend van een homogeen materiaal, dan komt een ronde vorm plots wel weer in aanmerking. Die ronde vorm treffen we trouwens aan in de banjo (een membraan als klankkast) en de Dobro-gitaar (metalen konus als klankkast).
Elasticiteitsmodulus, soortelijke massa en voortplantingssnelheid trillingen van enkele vaste stoffen:
| Stof | elasticiteitsmodulus bij 20° Celsius | soortelijke massa | voortplantingssnelheid trillingen |
| Metalen | |||
| staal | 196 - 216 kN/mm2 = 1.96E11 - 2.16E11 Pa | 7.3 kg/dm3 | 5181 m/s - 5439 m/s |
| GS-38 gietstaal | 210 kN/mm2 = 2.1E11 Pa | 7.25 kg/dm3 | 5382 m/s |
| GG15 zacht gietijzer | 80 - 90 kN/mm2 = 0.8E11 - 0.9E11 Pa | 7.25 kg/dm3 | ca. 3424 m/s |
| Aluminium (legering) | 60 - 80 kN/mm2 = 0.6E11 - 0.8E11 Pa | 2.7 kg/dm3 | 4714 m/s - 5443 m/s |
| Titanium legering (Grade 2) | 112 - 130 kN/mm2 = 1.12E11 - 1.3E11 Pa | 4.5 kg/dm3 | ca. 5163 m/s |
| Messing CuZn40 | 80 - 100 kN/mm2 = 0.8E11 -1E11 Pa | 8.4 - 8.7 kg/dm3 | ca. 3235 m/s |
| Messing - gegoten | 62 kN/mm2 = 0.62E11 Pa | 8.7 kg/dm3 | 2669 m/s |
| Messing, hard | 96.5kN/mm2 = 0.965E11 Pa | 8.44 kg/dm3 | 3381 m/s |
| Brons | 99.9kN/mm2 = 0.999E11 Pa | 7.4-8.9 kg/dm3 | 3675 - 3350 m/s |
| Fosforbrons | 8.8 kg/dm3 | ||
| CuSn8 | 85-90 kN/mm2 = 0.85E11 - 0.9E11 Pa | 7.4 - 8.9 kg/dm3 | ca. 3286 m/s |
| Goud (Au) | 19.32 kg/dm3 | ||
| Koper (Cu) | 8.93 kg/dm3 | ||
| Lood (Pb) | 5 kN/mm2 = 0.05E11 Pa | 11.35 kg/dm3 | 663.7 m/s |
| Nikkel (Ni) | 8.5 kg/dm3 | ||
| Tin (Sn) | 7.29 kg/dm3 | ||
| Platina (Pt) | 21 kg/dm3 | ||
| Zilver (Ag) | 10.45 kg/dm3 | ||
| Wolfraam (W) | 19.1 kg/dm3 | ||
| Iridium (Ir) | 528 GPa | 22.56 kg/dm3 | 4825 m/s |
| Osmium (Os) | 22.59 kg/dm3 | ||
| Steen en silicaten | |||
| Blauwsteen, graniet, kalksteen, marmer | 48 kN/mm2 = 0.48E11 Pa | 2.8 kg/dm3 | 4140 m/s |
| Zandsteen | 20 kN/mm2 = 0.2E11 Pa | ||
| Leisteen | 96.5 kN/mm2 = 0.965E11 Pa | 2.65 kg/dm3 | 6034 m/s |
| beton | 19.4 - 30.6 kN/mm2= 0.195E11-0.306E11 Pa | 2.3 kg/dm3 | 2911 - 3647 m/s |
| glas | 70 kN/mm2 = 0.7E11 Pa | 2.5 kg/dm3 | 5291 m/s |
| Houtsoorten | (Q in vezelrichting) | 0.2 - 1.3 kg/dm3 | |
| ahorn (esdoorn) | 0.681 kg/dm3 | ||
| berk | 0.664 kg/dm3 | ||
| beuk | 0.721 kg/dm3 | ||
| den | 9.2 - 9.9 kN/mm2 = 0.092E11 - 0.099E11 Pa | 0.599 kg/dm3 | Vv=3919 - 4065 m/s |
| ebbenhout | 1.259 kg/dm3 | ||
| ebeche (wawa) | |||
| eik | 10.3 - 10.8 kN/mm2=0.103E11 - 0.108E11 Pa | 0.785 kg/dm3 | Vv=1145 - 1173 m/s |
| els | 0.551 kg/dm3 | ||
| es | 0.692 kg/dm3 | ||
| haagbeuk | 0.776 kg/dm3 | ||
| linde | 0.489 kg/dm3 | ||
| lork | 0.519 kg/dm3 | ||
| wilde kastanje | 0.580 kg/dm3 | ||
| kerselaar | 0.647 kg/dm3 | ||
| mahonie | 0.813 kg/dm3 | ||
| notelaar | 0.735 kg/dm3 | ||
| perelaar | 0.689 kg/dm3 | ||
| populier | 0.472 kg/dm3 | ||
| olm | 0.626 kg/dm3 | ||
| vurenhout | 0.583 kg/dm3 | ||
| wilg | 0.486 kg/dm3 | ||
| Kunststoffen | |||
noteer: 1 Pa = 1N/m2
De cijfers in bovenstaande tabel (ze zal later verder worden uitgebreid, naarmate we bronnen kunnen aanboren) hebben we uit heel diverse bronnen samengebracht. De kleuren van de stof-beschrijving verwijzen naar de gebruikte bron.
bron: Ulrich Fisher (ed.), "Tabellenbuch Metall", Europa-Lehrmittel Verlag, Wuppertal, 1987, ISBN 3-8085-1086-2
bron: Max Fogiel (ed.), "The strength of materials & mechanics of solids problem solver", REA, New Jersey,1990, ISBN 0-87891-522-2
In sommige vooral angelsaksische literatuur treffen we helaas soms nog de elasticiteitsmodulus (Young's modulus) aan uitgedrukt in volkomen prehistorische eenheden: pond per vierkante duim... (lb/inch^2). Aangezien zo'n antiek pond overeenkomt met een gewicht van 453.591g en omdat 1g op het oppervlak van de aarde een (zwaarte)kracht ondergaat van 9.81E-3 Newton, terwijl een vierkante duim overeenkomt met 645.16 mm^2, kunnen we die cijfers omrekenen door ze te vermenigvuldigen met 6.897E-6. Soortelijke massa uitgedrukt in pond per kubieke voet rekenen we om naar kg/dm3 door te vermenigvuldigen met 0.016.
bron: Anoniem, Vlaamse bouw en aanbestedingskalender, ed. de bouwkroniek, Antwerpen 1950.
bron: VAN DIJKE, A.L. e.a., 'Materialenkennis', Ed.A.Kemperman, Haarlem 1947.
Vloeistoffen:
De empirische formule -een derde graadsvergelijking - voor de berekening van de voortplantingssnelheid van trillingen in water, rekening houdend met meerdere parameters is:
v = 1.449 + 4.6t - 0.055.t^2 + 0.003t^3 + (1.39 - 0.012t).(s-35) + 0.017d
waarin: s= zoutgehalte van het water in promille, d= diepte onder het wateroppervlak in meter, t = temperatuur in graden Celsius.
Meer gegevens over trillingen onder water zijn te vinden in:
Gregory HAINES, "Sound Underwater", ed. David & Charles Ltd, Devon, 1974, ISBN 0-8448-0302-2
Filedate: 2007- last updated: 2013-07-30
|
Terug naar inhoudstafel kursus: <Index Kursus> |
bibliografie en verdere lektuur m.b.t. akoestiek |
Naar homepage dr.Godfried-Willem RAES |
robots (katalogus muziekautomaten) |