Stemmingen en temperamenten

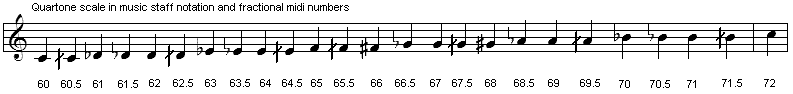
Dr.Godfried-Willem RAES

Stemmingen en Temperamenten

Hogeschool Gent : Departement Muziek. Vakgroep Scheppende Muziek

INLEIDING

KLASSIEKE EN ALTERNATIEVE TOONSYSTEMEN

Voor de eenduidige aanduiding van noten en tonen hanteren we het MIDI systeem, waarbij de centrale Do op het pianoklavier het nummer 60 krijgt. Bij een eerste benadering van het MIDI-systeem valt het op dat het in de allereerste plaats opgezet is voor westerse muziek, geschreven in gelijkzwevende toonsystemen. In Amerikaanse vakliteratuur wordt de gelijkzwevende stemming vaak aangeduid met de afkorting EQ (Equal) of ET (Equal Temperament). De nootnummer-kodes hebben in elk geval steeds betrekking op de ermee overeenstemmende noten op het normale moderne pianoklavier.

Omdat het voor een goed begrip van hetgeen volgt nogal belangrijk is, toch eerst even een opfrissing met betrekking tot de preciese wiskundige basis van het gelijkzwevend toonsysteem :

regel 1 :

gegeven Fo = een bepaalde toonhoogte, dan is Fo * 2 = het oktaaf daarboven en Fo / 2 = het oktaaf eronder.

Elke oktavering van een toonhoogte komt dus heel precies overeen met een verdubbeling resp. halvering van haar trillingsgetal. De deelfaktoren zijn machten van twee. Toonhoogte kent derhalve geen lineair, maar een kwadratisch verloop.

regel 2 :

elk oktaaf zal worden verdeeld in 12 precies gelijke intervallen (halve tonen, in het westers jargon) en wel op volgende wiskundige wijze :

interval = (2^(1/12)). Dit is de twaalfdemachtswortel uit 2. We verdelen een oktaaf (een verdubbeling) in 12 gelijke mootjes.

F0 = F0 * (2^(0/12)) = F0
F1 = F0 * (2^(1/12)) = F0 * 1.05946309436
F2 = F0 * (2^(2/12))
F3 = F0 * (2^(3/12))
...
...
Fn = F0 * (2^(n/12))
...
F12 = F0 * (2^(12/12)) = F0 * 2

Zo verkrijgen we alle toonhoogtes waaruit de kromatische toonladder is opgebouwd.

Deze verdeling van het oktaaf in twaalf gelijke delen werd het ultieme antwoord van de muziekkultuur op het equivalent van de kwadratuur van de cirkel voor de muziek: met name, de onmogelijkheid van de kwintencirkel. Inderdaad, wanneer we kwinten (het halve drievoud van de basisfrekwentie) opstapelen, komen we nooit opnieuw bij dezelfde toon uit. Dit volgt uit de rekenkundige evidentie dat (3/2)^12 = 129,7 en niet = 128. Voor geen enkele gehele macht van 3/2 krijgen we ooit een macht van twee als resultaat. Anders gesteld: de kwintencirkel bestaat niet maar is veeleer een kwintenspiraal, die bij elke omwenteling een nieuwe reeks intervallen genereert zonder ooit naar haar oorsprong terug te keren. Het antwoord van de gelijkzwevende stemming was (2^(1/12))^12 = 2. De cirkel sluit nu, maar alle intervalverhoudingen zijn irrationale getallen geworden.

OPMERKING:

De notatie hier is die zoals gebruikt in programmeertalen zoals BASIC en Fortran. Hierbij wordt een n-de machtwortel uit een getal genoteerd als het tot de 1/n-breuk verheffen van dat getal.

vb. vierkantswortel 2 = 2^(1/2), derdemachtswortel uit 10 = 10^(1/3)

Het immense voordeel van deze notatie tegenover de traditionele is dat alle bewerkingen nu in gewoon machineschrift kunnen worden weergegeven, zonder gebruik te moeten maken van ingewikkelde grafische tekens en speciale wetenschappelijke tekstverwerkers zoals 'Tex'.

Het zal de aandachtige student wel opvallen dat het getal 2 dat zich hier telkens onder de wortel bevindt, voortkomt uit het feit dat we een verdubbeling van frekwentie (*2), een oktaaf dus, in gelijke stukjes wilden verdelen. Het is perfekt mogelijk een toonsysteem te bedenken dat bvb. vrij is van oktaven , of, dat bvb. slechts om de twee oktaven terug juiste oktaven oplevert ... Denk bvb. eens aan de mogelijkheid een interval van twee oktaven te gaan verdelen in 15 gelijke intervallen! De juiste noodzakelijke toonhoogtes kunnen we dan berekenen alsvolgt:

F0 = F0
F1 = F0 * (4^(1/15))
...
Fn = F0 * (4^(n/15))
F15 = F0 * (4^(15/15)) = F0 * 4

We geven dit voorbeeld alleen om erop te wijzen dat ons gelijkzwevend toonsysteem eigenlijk slechts een van de zeer vele mogelijke gelijkzwevende systemen is. In verdere paragrafen gaan we daar veel dieper op in.

Een gelijkzwevend kwarttoonssysteem kan worden berekend met fo * (2^(n/24)), waarbij n gaat van 0 tot 24, voor alle frekwenties binnen een oktaaf. De bekende Fokker-Huygens stemming, die kwa reinheid de juisteboventoonsstemming (zie verder) erg dicht benaderd, en op grond waarvan toch heel wat instrumenten (o.m. een nederlands pijporgel) zijn gebouwd, gaat uit van een verdeling van het oktaaf in 31 delen. Dat is dus:

fo * (2^(n/31)), voor n =0 tot 31

De algemene vorm van alle gelijkzwevende systemen is evenwel steeds dezelfde:

stap 1 (regel 1): bepaal het interval waarbinnen een toonreeks gelijkzwevend verdeeld dient te worden. (Noteer: het hoeven niet eens oktaven te zijn!). Stel interval= x.

stap 2 (regel 2): bepaal het aantal verdelingen waarover je binnen dat interval wil kunnen beschikken. Stel verdeling = Notes.

F0 = F0

Fn = F0 * ( Interval^(n/Notes))

De teoretici van de muzikale akoestiek en de harmonie, hebben om het getemperd systeem toch te kunnen afwegen tegenover andere mogelijke etnische en oudere (maar daarom niet verouderde...) systemen, nog een ekstra eenheid ingevoerd, kleiner dan het kleinste interval binnen het 12-tonig gelijkzwevend systeem (de halve toon). Om deze frakties te bepalen hebben zij de toonsafstand van een halve toon in elk interval verdeeld in honderd gelijkzwevende stukjes, die men CENT noemt. Voor hondersten, en dus niet bvb. door duizendsten, heeft men gekozen omdat een honderdste van een halve tooninterval reeds niet meer voor het menselijk oor te onderscheiden valt. Aangezien het in muziek toch steeds om geluiden voor en door menselijke waarnemers gaat, niet zo'n gek uitgangspunt natuurlijk. In Cent uitgedrukt wordt het oktaaf dus verdeeld in 1200 gelijke stukjes.

Wiskundig ziet dat er dan uit alsvolgt :

F(n) = F0 * (2^(n/1200))

vb. stel LA=440 Hz en Sib=466 Hz, dan is in dit interval 100 Cents = 466-440 = 26 Hz

Dat het aantal trillingen dat met 100 Cents overeenkomt verschilt naargelang het beschouwde interval zal wel duidelijk zijn wanneer we nu een ander interval bezien:

stel LA=1760 Hz en Sib=1864 Hz dan worden 100 cents hier = 1864 -1760= 104 Hz

Rekening houdend hiermee en met de praktische relevantie van al te kleine sowieso onhoorbare frakties, mogen we de Cents-verdeling echter gerust lineair interpolleren. Wanneer we het MIDI-kodesysteem willen uitbreiden zodat het bruikbaar wordt voor het werken met andere stemmingen (steeds uitgaande van de 12-toons gelijkzwevende stemming als referentiepunt) dan volstaat het de afwijking in cents van een gegeven toon te noteren als het deel achter de komma bij de overeenstemmende toon. 60.5 wordt dan een met een kwarttoon verhoogde centrale Do.

Door de introduktie van deze nieuwe eenheid werd het mogelijk een muzikaal inzicht te krijgen in bvb. de relatie van de (niet-getemperde, maar daarom nog niet noodzakelijk écht korrekte) boventoonreeks van snaren en blaasinstrumenten tot de noten van het gelijkzwevend systeem. Lees er maar onze hoofdstukken over akoestiek van muziekinstrumenten (snaren, pijpen, staven en membranen) op na.

Voorbeeld:

een akoestisch perfekte reine kwint is hierdoor gekenmerkt dat de trillingsgetallen der beide toonhoogtes zich verhouden als 3 tot 2.

Een rekenkundig perfekte kwint op DO = 523 Hz levert dan ook op

SOL = 523*3/2 = 784.5 Hz

Een gelijkzwevende kwint op Do =523 Hz echter is :

F(7) = 523 * (2^(7/12)) = 783.6 Hz

De gelijkzwevende kwint is dus een beetje te laag in vergelijking met de 'natuurlijke', of beter gezegd 'rekenkundige' kwint. Laten we beide toonhoogten gelijktijdig horen, dan horen we zwevingen met een frekwentie van 784.5 - 783.6 = 0.9Hz, of iets minder dan 1 zweving per sekonde. Merk op dat we dit bij het stemmen van een piano bvb., waarnemen als ongeveer 2 (ritmische) zwevingen per sekonde, wat echter veroorzaakt wordt door de zwevingen van de boventonen:

de tweede harmonische (of oktaaf) van de getemperde Sol= 1567.2 Hz (= 2 x 783.6Hz) 784.5Hz is het oktaaf, dus: 1569Hz.
de derde harmonische (de kwint boven het oktaaf) van Do = 1569.0Hz

wanneer die samen klinken horen we 1.8 zwevingen per sekonde.

Een berekening in Cents (hier met lineaire interpollatie):

De getemperde Fa# = F(6)=523 * (2^(6/12)) = 740 Hz

Sol = 783.6 Hz

100 Cents = 43.6 Hz en dus 1 Cent = 0.436 Hz

Juiste kwint Sol = 784.5 Hz

Verschil met getemperde sol = 783.6-784.5 = - 0.9 Hz

Verschil in Cents = 0.9/0.436 = - 2 Cents

Het zijn deze eenheden die steeds weer worden gebruikt bij onderlinge vergelijkingen van diverse toonsystemen en die men dan ook in de technische literatuur terzake kan weervinden. Niet getemperde systemen berusten zowat allemaal op 'juiste' boventoonsreeksen. Wiskundig komt dat erop neer dat alle intervallen kwalitatief verschillend zijn, want afgeleid uit eenvoudige getalverhoudingen ten opzichte van een willekeurig gekozen grondtoon.

Welhaast klassieke, niet getemperde noch gelijkzwevende, toonsystemen zijn bvb.:

De juiste boventoons-grote-terstoonladder :

DO	RE	MI	FA	SOL	LA	SI	DO
Fo	Fo * 9/8	Fo * 5/4	Fo * 4/3	Fo * 3/2	Fo * 5/3	Fo * 15/8	Fo * 2

De onderlinge getalverhoudingen der intervallen zijn daarbij dan :

DO - RE

RE -MI

MI - FA

FA - SOL

SOL - LA

LA -SI

SI -DO

(9:8)/(1:1)= 9:8

(5:4)/(9:8) = 10: 9

(4:3) / (5:4) = 16:15

(3:2) / (4:3) = 9:8

(5:3)/ (3:2) =10:9

(15:8)/(5:3) = 9:8

(1:2)/(15:8) = 16:15

De juiste boventoons-mineur-toonladder :

DO	RE	MI	FA	SOL	LA	SI	DO
Fo	Fo * 9/8	Fo * 6/5	Fo * 4/3	Fo * 3/2	Fo * 8/5	Fo * 9/5	Fo * 2

Intervallen in deze juiste boventoons mineur toonladder:

DO - RE

RE -MI

MI - FA

FA - SOL

SOL - LA

LA -SI

SI -DO

9:8

16:15

10:9

9:8

16:15

9:8

10:9

Vanzelfsprekend zijn ook hier weer onnoemelijk vele alternatieve mogelijkheden voorhanden om onze oktaven te gaan verdelen. De vele muziekkulturen die onze wereld kent (of gekend heeft, want vele ervan werden door het imperialisme van onze muziekkultuur en haar speeltuigen zo goed als uitgeroeid) hebben bijna evenzoveel verschillende toonsystemen voortgebracht. Verder geven we zowat alle realistische mogelijkeden en gaan we ook wat dieper in op een aantal voor de recente muziekgeschiedenis relevante selekties.

ANALYSE VAN GELIJKZWEVENDE TOONSYSTEMEN

Alle hier uitgevoerde berekeningen gaan uit van diapason La = 440.0Hz Noten worden uitgedrukt als fraktionele midi getallen, waarbij noot 60 overeenkomt met de centrale Do (C) op het pianoklavier.

Kwintenspiralen: 
Reine kwinten (3:2)
fout in cents: 1            aantal kwinten= 665 (aantal kwinten nodig om met 1 cent nauwkeurigheid te sluiten)
fout in cents: 2            aantal kwinten= 359 
fout in cents: 4            aantal kwinten= 53 
fout in cents: 24           aantal kwinten= 12  (de eerste periode van de kwintenspiraal)
De afwijking bij 12 tonen, benaderd de historische syntonische komma= 200/9 = 22.2

De gelijkzwevend verkregen intervallen kunnen we nu vergelijken met de juiste boventoonsintervallen:
In het 12-tonig gelijkzwevend systeem:

Juistheid van de 6:5 kleine terts in cent:  15.64  2 ^ ( 3/ 12). Interval: 60   63
Juistheid van de 5:4 grote terts in cent:  -13.69  2 ^ ( 4/ 12). Interval: 60   64
Juistheid van de 4:3 kwart in cent:         -1.95  2 ^ ( 5/ 12). Interval: 60   65
Juistheid van de 3:2 kwint in cent:          1.96  2 ^ ( 7/ 12). Interval: 60   67

In het 53 tonig gelijkzwevend systeem daareentegen:

Juistheid van de 6:5 kleine terts in cent:  -1.34  2 ^ ( 14/ 53). Interval: 60   63.16981
Juistheid van de 5:4 grote terts in cent:    1.41  2 ^ ( 17/ 53). Interval: 60   63.84906
Juistheid van de 4:3 kwart in cent:          -.07  2 ^ ( 22/ 53). Interval: 60   64.98113
Juistheid van de 3:2 kwint in cent:           .07  2 ^ ( 31/ 53). Interval: 60   67.01887

Dat een 53 toons systeem merkelijk juistere intervallen oplevert, hoeft geen betoog. De kwinten zijn perfekt en de tertsen volstrekt harmonisch. Een gelijkzwevend toonsysteem met 54 tonen per oktaaf zou evenwel leiden tot volstrekt niet hanteerbare, laat staan praktisch stembare, akoestische muziekinstrumenten. Elektronisch vormt het dan weer geen enkel probleem. De weinige komposities die dan ook in een 53 toons gelijkzwevende stemming zijn geschreven en gerealiseerd, behoren allemaal tot de elektronische muziek.

Ongebruikelijk in onze klassieke muziek, maar rekenkundig perfekt mogelijk, kunnen we ook uitgaan van kwartencirkels, met als resultaat:

  
Reine kwarten (4:3) spiralen
fout in cents: 1            aantal kwarten= 7621 
fout in cents: 2            aantal kwarten= 306 
fout in cents: 6            aantal kwarten= 253 
fout in cents: 9            aantal kwarten= 200 
fout in cents: 13           aantal kwarten= 147 
fout in cents: 17           aantal kwarten= 94 
fout in cents: 20           aantal kwarten= 41 
fout in cents: 44           aantal kwarten= 29 
fout in cents: 67           aantal kwarten= 17

Dit zouden leiden tot een oktaafverdeling in 17, 29 of 41 delen, maar zoals blijkt uit de berekening levert dit geenszins een beter resultaat op dan een kwintenstemming. We hebben 41 intervallen per oktaaf nodig om de kwartenspiraal als cirkel te doen sluiten met een afwijking iets kleiner dan de komma.

Juistheid van de 6:5 kleine terts in cent: -6.31  2 ^ ( 11/ 41). Interval: 60   63.21952
Juistheid van de 5:4 grote terts in cent:   5.83  2 ^ ( 13/ 41). Interval: 60   63.80488
Juistheid van de 4:3 kwart in cent:          .48  2 ^ ( 17/ 41). Interval: 60   64.97561
Juistheid van de 3:2 kwint in cent:         -.48  2 ^ ( 24/ 41). Interval: 60   67.02439

De verdeling van het oktaaf in zeventien intervallen, uitgaand van kwarten levert:

Juistheid van de 6:5 kleine terts in cent:  33.29  2 ^ ( 4/ 17). Interval: 60   62.82353
Juistheid van de 5:4 grote terts in cent:   33.37  2 ^ ( 5/ 17). Interval: 60   63.52942
Juistheid van de 4:3 kwart in cent:          3.93  2 ^ ( 7/ 17). Interval: 60   64.94118
Juistheid van de 3:2 kwint in cent:         -3.93  2 ^ ( 10/ 17). Interval: 60  67.05883

Hier stellen we vast dat ondanks een grotere verdeling van het oktaaf, er helemaal geen voordeel kan gehaald worden uit een dergelijke stemming. De kwinten zijn slechter en ook de tertsen wijken sterker af dan in de gewone 12-tonige gelijkzwevende stemming.

Opdat de intervallencirkel zich binnen een redelijk aantal cycli zou sluiten, is het vereist dat het cirkelinterval geen deler is of gemeenschappelijk heeft met 12, teminste voorzover we een toonsysteem willen waarin konventionele muziek nog steeds redelijk speelbaar blijft... Op grond hiervan zouden we dan ook een systeem kunnen baseren op de juiste grote septiem.

Grote septiemen (15:8) spiralen 
fout in cents: 1            aantal 15:8 septiemen= 537 
fout in cents: 3            aantal 15:8 septiemen= 247 
fout in cents: 7            aantal 15:8 septiemen= 204 
fout in cents: 12           aantal 15:8 septiemen= 161 
fout in cents: 16           aantal 15:8 septiemen= 118 
fout in cents: 21           aantal 15:8 septiemen= 75 
fout in cents: 25           aantal 15:8 septiemen= 32 
fout in cents: 54           aantal 15:8 septiemen= 21 
 
Juistheid van de 6:5 kleine terts in cent:   -27.22  2 ^ ( 6/ 21). Interval: 60   63.42857
Juistheid van de 5:4 grote terts in cent:    -13.69  2 ^ ( 7/ 21). Interval: 60   64
Juistheid van de 4:3 kwart in cent:          -16.24  2 ^ ( 9/ 21). Interval: 60   65.14285
Juistheid van de 3:2 kwint in cent:           16.24  2 ^ ( 12/ 21). Interval: 60  66.85714

Waarom dit nooit aanleiding gaf tot praktische muziek, zal wel duidelijk zijn...
Evenmin gebruikelijk, maar bepleitbaar, zou zijn een stemming te steunen op zo juist mogelijke grote (5:4) of kleine (6:5) tertsen:

Grote juiste tertsen (5:4) spiralen
fout in cents: 1            aantal 5:4 tertsen= 2075 
fout in cents: 2            aantal 5:4 tertsen= 146 
fout in cents: 10           aantal 5:4 tertsen= 87 
fout in cents: 17           aantal 5:4 tertsen= 28 
fout in cents: 58           aantal 5:4 tertsen= 25 
fout in cents: 99           aantal 5:4 tertsen= 22 
   
Juistheid van de 6:5 kleine terts in cent: -11.63  2 ^ ( 6/ 22). Interval: 60   63.27273
Juistheid van de 5:4 grote terts in cent:    4.5  2 ^ ( 7/ 22).  Interval: 60   63.81818
Juistheid van de 4:3 kwart in cent:          7.14  2 ^ ( 9/ 22). Interval: 60   64.90909
Juistheid van de 3:2 kwint in cent:         -7.14  2 ^ ( 13/ 22).Interval: 60   67.09091

Uitgaand van een grote tertsen-stemming, krijgen we dus wanneer we een oktaaf verdelen in 22 gelijke delen, een tertsen-spiraal die ons op 1 cent na, naar een een halve toon verschoven toonsysteem brengt. Zo'n systeem zou dus te verzoenen zijn met het kromatisch 12-tonig gelijkzwevend systeem, maar dan met goede tertsen ten nadele van nogal botsende kwinten.

We kunnen op gelijkaardige wijze ook nog berekenen wat kleine tertsen (6:5) ons kunnen bieden, maar met een minimale onderverdeling van het oktaaf in 23 intervallen sluiten we nog steeds af met een fout van 60 cents...

Juistheid van de 6:5 kleine terts in cent:  2.6    2 ^ ( 6/ 23). Interval:  60   63.13044
Juistheid van de 5:4 grote terts in cent:  21.1    2 ^ ( 7/ 23). Interval:  60   63.65218
Juistheid van de 4:3 kwart in cent:       -23.69   2 ^ ( 10/ 23). Interval: 60   65.21739
Juistheid van de 3:2 kwint in cent:        23.69   2 ^ ( 13/ 23). Interval: 60   66.78261

De gelijkzwevende 19 toons verdeling van het oktaaf heeft een grote graad van perfektie bereikt voor de harmonische juistheid van de kleine tertsen. De 'onreinheid' van de grote tertsen, de kwarten en de kwinten is hier precies evengroot. Het is een stemming die heel wat verdedigers heeft gehad. (Er bestaat ook een 19-toons niet gelijkzwevende variant).

Juistheid van de 6:5 kleine terts in cent:   -.15  2 ^ ( 5/ 19). Interval:  60   63.1579
Juistheid van de 5:4 grote terts in cent:    7.37  2 ^ ( 6/ 19). Interval:  60   63.78947
Juistheid van de 4:3 kwart in cent:         -7.22  2 ^ ( 8/ 19). Interval:  60   65.05264
Juistheid van de 3:2 kwint in cent:          7.22  2 ^ ( 11/ 19). Interval: 60   66.94737

Uit bovenstaande berekeningen en overwegingen blijkt de op kwinten gesteunde gelijkzwevende stemming voor een 12 tonige verdeling van het oktaaf alleszins nog het meest ekonomisch en rationeel te zijn.

Maar, in plaats van uit te gaan van een enkel interval dat we zo dicht mogelijk bij het platonische ideaal laten aanleunen, -meestal is dat de kwint- kunnen we ook pogen een optimalisatie te vinden waarbij zoveel mogelijk van de diatonische intervallen 'juist' klinken. Dit is precies wat Huygens en Fokker voor ogen stond bij de ontwikkeling van de door hen voorgestelde gelijkzwevende stemming met 31-tonen per oktaaf.

Juistheid van de 6:5 kleine terts in cent:  5.96  2 ^ ( 8/ 31).  Interval: 60   63.09678
Juistheid van de 5:4 grote terts in cent:   -.78  2 ^ ( 10/ 31). Interval: 60   63.87097
Juistheid van de 4:3 kwart in cent:        -5.18  2 ^ ( 13/ 31). Interval: 60   65.03226
Juistheid van de 3:2 kwint in cent:         5.18  2 ^ ( 18/ 31). Interval: 60   66.96774

Maar, het is ook mogelijk een heel andere weg in te slaan. In plaats van het oktaaf te verdelen in twaalf gelijkzwevende delen, kunnen we ook de duodeciem (oktaaf + kwint) gelijkzwevend verdelen in 19 halvetoons intervallen. Dit levert ons vanzelfsprekend opnieuw een stemming op met 12 tonen per oktaaf, dus volkomen kompatibel met de organisatie van de bestaande westerse muziekinstrumenten met klavieren en fretten. Het voordeel is dat we dan steeds juiste kwinten hebben, maar de oktaven iets aan juistheid inboeten. In de laatste jaren gaan -vooral in Frankrijk- meer en meer stemmen op om onze pianos en orkestinstrumenten op deze wijze te gaan stemmen en intoneren.
We hebben beide systemen naasteen berekend en in volgende tabel tegenover elkaar gesteld:

Vergelijking gelijkzwevende verdeling oktaaf in 12 delen, of duodeciem in 19 delen, eveneens gelijkzwevend, met opgave van de exakte frekwenties van de zo verkregen kromatische toonhoogtes.

noot= 24 12-root 2 freq= 32.7032 19-root 3 freq= 32.7032 noot= 25 12-root 2 freq= 34.64783 19-root 3 freq= 34.64989 noot= 26 12-root 2 freq= 36.7081 19-root 3 freq= 36.71247 noot= 27 12-root 2 freq= 38.89088 19-root 3 freq= 38.89782 noot= 28 12-root 2 freq= 41.20345 19-root 3 freq= 41.21325 noot= 29 12-root 2 freq= 43.65354 19-root 3 freq= 43.66651 noot= 30 12-root 2 freq= 46.24931 19-root 3 freq= 46.26581 noot= 31 12-root 2 freq= 48.99944 19-root 3 freq= 49.01983 noot= 32 12-root 2 freq= 51.9131 19-root 3 freq= 51.93779 noot= 33 12-root 2 freq= 55.00001 19-root 3 freq= 55.02944 noot= 34 12-root 2 freq= 58.27048 19-root 3 freq= 58.30512 noot= 35 12-root 2 freq= 61.73542 19-root 3 freq= 61.7758	noot= 72 12-root 2 freq= 523.2512 19-root 3 freq= 524.7461 noot= 73 12-root 2 freq= 554.3654 19-root 3 freq= 555.9822 noot= 74 12-root 2 freq= 587.3296 19-root 3 freq= 589.0776 noot= 75 12-root 2 freq= 622.2541 19-root 3 freq= 624.1431 noot= 76 12-root 2 freq= 659.2552 19-root 3 freq= 661.2958 noot= 77 12-root 2 freq= 698.4566 19-root 3 freq= 700.6602 noot= 78 12-root 2 freq= 739.989 19-root 3 freq= 742.3677 noot= 79 12-root 2 freq= 783.991 19-root 3 freq= 786.558 noot= 80 12-root 2 freq= 830.6096 19-root 3 freq= 833.3787 noot= 81 12-root 2 freq= 880.0001 19-root 3 freq= 882.9864 noot= 82 12-root 2 freq= 932.3277 19-root 3 freq= 935.5471 noot= 83 12-root 2 freq= 987.7668 19-root 3 freq= 991.2366
noot= 36 12-root 2 freq= 65.4064 19-root 3 freq= 65.45307 noot= 37 12-root 2 freq= 69.29567 19-root 3 freq= 69.34923 noot= 38 12-root 2 freq= 73.41621 19-root 3 freq= 73.47732 noot= 39 12-root 2 freq= 77.78176 19-root 3 freq= 77.85114 noot= 40 12-root 2 freq= 82.40691 19-root 3 freq= 82.4853 noot= 41 12-root 2 freq= 87.30708 19-root 3 freq= 87.39533 noot= 42 12-root 2 freq= 92.49862 19-root 3 freq= 92.59763 noot= 43 12-root 2 freq= 97.99888 19-root 3 freq= 98.1096 noot= 44 12-root 2 freq= 103.8262 19-root 3 freq= 103.9497 noot= 45 12-root 2 freq= 110 19-root 3 freq= 110.1374 noot= 46 12-root 2 freq= 116.541 19-root 3 freq= 116.6934 noot= 47 12-root 2 freq= 123.4708 19-root 3 freq= 123.6397	noot= 84 12-root 2 freq= 1046.502 19-root 3 freq= 1050.241 noot= 85 12-root 2 freq= 1108.731 19-root 3 freq= 1112.758 noot= 86 12-root 2 freq= 1174.659 19-root 3 freq= 1178.996 noot= 87 12-root 2 freq= 1244.508 19-root 3 freq= 1249.177 noot= 88 12-root 2 freq= 1318.51 19-root 3 freq= 1323.535 noot= 89 12-root 2 freq= 1396.913 19-root 3 freq= 1402.32 noot= 90 12-root 2 freq= 1479.978 19-root 3 freq= 1485.795 noot= 91 12-root 2 freq= 1567.982 19-root 3 freq= 1574.238 noot= 92 12-root 2 freq= 1661.219 19-root 3 freq= 1667.946 noot= 93 12-root 2 freq= 1760 19-root 3 freq= 1767.233 noot= 94 12-root 2 freq= 1864.655 19-root 3 freq= 1872.429 noot= 95 12-root 2 freq= 1975.534 19-root 3 freq= 1983.888
noot= 48 12-root 2 freq= 130.8128 19-root 3 freq= 130.9995 noot= 49 12-root 2 freq= 138.5913 19-root 3 freq= 138.7974 noot= 50 12-root 2 freq= 146.8324 19-root 3 freq= 147.0595 noot= 51 12-root 2 freq= 155.5635 19-root 3 freq= 155.8134 noot= 52 12-root 2 freq= 164.8138 19-root 3 freq= 165.0883 noot= 53 12-root 2 freq= 174.6142 19-root 3 freq= 174.9154 noot= 54 12-root 2 freq= 184.9972 19-root 3 freq= 185.3274 noot= 55 12-root 2 freq= 195.9978 19-root 3 freq= 196.3592 noot= 56 12-root 2 freq= 207.6524 19-root 3 freq= 208.0477 noot= 57 12-root 2 freq= 220 19-root 3 freq= 220.432 noot= 58 12-root 2 freq= 233.0819 19-root 3 freq= 233.5534 noot= 59 12-root 2 freq= 246.9417 19-root 3 freq= 247.4559	noot= 96 12-root 2 freq= 2093.005 19-root 3 freq= 2101.981 noot= 97 12-root 2 freq= 2217.461 19-root 3 freq= 2227.103 noot= 98 12-root 2 freq= 2349.319 19-root 3 freq= 2359.674 noot= 99 12-root 2 freq= 2489.016 19-root 3 freq= 2500.136 noot= 100 12-root 2 freq= 2637.021 19-root 3 freq= 2648.959 noot= 101 12-root 2 freq= 2793.826 19-root 3 freq= 2806.641 noot= 102 12-root 2 freq= 2959.956 19-root 3 freq= 2973.71 noot= 103 12-root 2 freq= 3135.964 19-root 3 freq= 3150.723 noot= 104 12-root 2 freq= 3322.438 19-root 3 freq= 3338.273 noot= 105 12-root 2 freq= 3520 19-root 3 freq= 3536.987 noot= 106 12-root 2 freq= 3729.311 19-root 3 freq= 3747.53 noot= 107 12-root 2 freq= 3951.067 19-root 3 freq= 3970.606
noot= 60 12-root 2 freq= 261.6256 19-root 3 freq= 262.186 noot= 61 12-root 2 freq= 277.1827 19-root 3 freq= 277.7929 noot= 62 12-root 2 freq= 293.6648 19-root 3 freq= 294.3288 noot= 63 12-root 2 freq= 311.127 19-root 3 freq= 311.8491 noot= 64 12-root 2 freq= 329.6276 19-root 3 freq= 330.4122 noot= 65 12-root 2 freq= 349.2283 19-root 3 freq= 350.0803 noot= 66 12-root 2 freq= 369.9945 19-root 3 freq= 370.9192 noot= 67 12-root 2 freq= 391.9955 19-root 3 freq= 392.9986 noot= 68 12-root 2 freq= 415.3048 19-root 3 freq= 416.3923 noot= 69 12-root 2 freq= 440.0001 19-root 3 freq= 441.1784 noot= 70 12-root 2 freq= 466.1638 19-root 3 freq= 467.4401 noot= 71 12-root 2 freq= 493.8834 19-root 3 freq= 495.2649	noot= 108 12-root 2 freq= 4186.01 19-root 3 freq= 4206.96 noot= 109 12-root 2 freq= 4434.923 19-root 3 freq= 4457.384 noot= 110 12-root 2 freq= 4698.637 19-root 3 freq= 4722.715 noot= 111 12-root 2 freq= 4978.033 19-root 3 freq= 5003.84 noot= 112 12-root 2 freq= 5274.042 19-root 3 freq= 5301.699 noot= 113 12-root 2 freq= 5587.653 19-root 3 freq= 5617.288 noot= 114 12-root 2 freq= 5919.912 19-root 3 freq= 5951.662 noot= 115 12-root 2 freq= 6271.928 19-root 3 freq= 6305.942 noot= 116 12-root 2 freq= 6644.876 19-root 3 freq= 6681.31 noot= 117 12-root 2 freq= 7040.001 19-root 3 freq= 7079.022 noot= 118 12-root 2 freq= 7458.622 19-root 3 freq= 7500.408 noot= 119 12-root 2 freq= 7902.134 19-root 3 freq= 7946.878 noot= 120 12-root 2 freq= 8372.02 19-root 3 freq= 8419.924

Ter beoordeling hierbij een 'graad'meter van de kwaliteit van de duodeciem stemming:

Juistheid van de 6:5 kleine terts in cent:  15.33  3 ^ ( 3/ 19). Interval: 60   63.00309
Juistheid van de 5:4 grote terts in cent:   -14.1  3 ^ ( 4/ 19). Interval: 60   64.00412
Juistheid van de 4:3 kwart in cent:         -2.47  3 ^ ( 5/ 19). Interval: 60   65.00515
Juistheid van de 3:2 kwint in cent:          1.24  3 ^ ( 7/ 19). Interval: 60   67.0072
Juistheid van de 2:1 oktaaf in cent:        -1.24  3 ^ ( 12/ 19).Interval: 60   72.01235

In vergelijking met de konventionele stemming met juiste oktaven, levert deze stemming ons inderdaad substantieel betere kwinten op. De oktaven worden nu iets te klein genomen. Verder bij onze behandeling van reeele boventonen van snaren zal blijken dat hiervoor zeer sterke wetenschappelijke argumenten te geven zijn. De heilige koe van het juiste oktaaf wordt hier evenwel geofferd...

KWARTTOONSSYSTEMEN EN STEMMINGEN

Kwarttoons gelijkzwevende stemmingen hebben in de loop van de geschiedenis tot op vandaag vele pleitbezorgers gekend. Charles Ives, Yvan Wiesnegradsky en Alois Haba zijn wellicht de bekendste voorbeelden uit de eerste helft van de twintigste eeuw. Er werden en worden ook heel wat instrumenten speciaal voor gebouwd en ontworpen. Wijzelf hebben voor deze stemming een orgel gebouwd met een tessituur van zes oktaven, <Qt>, dit in het kader van een postdoktoraal onderzoeksprojekt van de Hogeschool Gent, departement Muziek en Drama, in samenwerking met Stichting Logos, waar een uitgebreid atelier voor experimentele instrumentenbouw en artistiek-technologische research operationeel is. Daarnaast bouwden we ook een kwarttoons xylofoon (3.5 oktaven), een kwarttoons-tubofoon (3 oktaven) en <puff>, (4 oktaven, eveneens in kwarttonen). De mogelijkheid om kwarttoonsmuziek op pianos te spelen hebben we eveneens, met behulp van de beide pianorobots die we in de laatste decennia tot een vrij grote graad van perfektie wisten te brengen. Redenen te over dus om hier wat nader in te gaan op kwarttoons stemmingen en de specifieke eigenschappen ervan.

Alle hier uitgevoerde berekeningen gaan uit van diapason La = 440.0Hz. Noten worden uitgedrukt als fraktionele midi getallen, waarbij noot 60 overeenkomt met de centrale Do (C) op het pianoklavier.

  
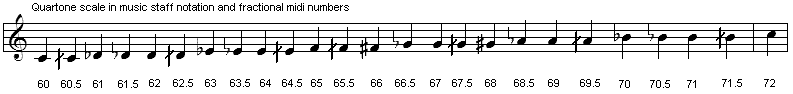
Kwarttoons gelijkzwevende stemmingen:
Vergelijking verdeling oktaaf in 24 delen, of duodeciem in 38 delen, gelijkzwevend

noot= 24 24-root 2 freq= 32.7032 38-root 3 freq= 32.7032 noot= 24.5 24-root 2 freq= 33.17888 38-root 3 freq= 33.17937 noot= 25 24-root 2 freq= 33.66148 38-root 3 freq= 33.66248 noot= 25.5 24-root 2 freq= 34.1511 38-root 3 freq= 34.15262 noot= 26 24-root 2 freq= 34.64783 38-root 3 freq= 34.64989 noot= 26.5 24-root 2 freq= 35.1518 38-root 3 freq= 35.15441 noot= 27 24-root 2 freq= 35.66309 38-root 3 freq= 35.66628 noot= 27.5 24-root 2 freq= 36.18182 38-root 3 freq= 36.18559 noot= 28 24-root 2 freq= 36.7081 38-root 3 freq= 36.71247 noot= 28.5 24-root 2 freq= 37.24203 38-root 3 freq= 37.24701 noot= 29 24-root 2 freq= 37.78373 38-root 3 freq= 37.78934 noot= 29.5 24-root 2 freq= 38.33331 38-root 3 freq= 38.33957 noot= 30 24-root 2 freq= 38.89088 38-root 3 freq= 38.89782 noot= 30.5 24-root 2 freq= 39.45656 38-root 3 freq= 39.46418 noot= 31 24-root 2 freq= 40.03047 38-root 3 freq= 40.0388 noot= 31.5 24-root 2 freq= 40.61272 38-root 3 freq= 40.62178 noot= 32 24-root 2 freq= 41.20345 38-root 3 freq= 41.21325 noot= 32.5 24-root 2 freq= 41.80277 38-root 3 freq= 41.81333 noot= 33 24-root 2 freq= 42.4108 38-root 3 freq= 42.42215 noot= 33.5 24-root 2 freq= 43.02768 38-root 3 freq= 43.03983 noot= 34 24-root 2 freq= 43.65354 38-root 3 freq= 43.66651 noot= 34.5 24-root 2 freq= 44.28849 38-root 3 freq= 44.30231 noot= 35 24-root 2 freq= 44.93268 38-root 3 freq= 44.94737 noot= 35.5 24-root 2 freq= 45.58624 38-root 3 freq= 45.60182	noot= 72 24-root 2 freq= 130.8128 38-root 3 freq= 130.9995 noot= 72.5 24-root 2 freq= 132.7155 38-root 3 freq= 132.9069 noot= 73 24-root 2 freq= 134.6459 38-root 3 freq= 134.8421 noot= 73.5 24-root 2 freq= 136.6044 38-root 3 freq= 136.8055 noot= 74 24-root 2 freq= 138.5913 38-root 3 freq= 138.7974 noot= 74.5 24-root 2 freq= 140.6072 38-root 3 freq= 140.8184 noot= 75 24-root 2 freq= 142.6524 38-root 3 freq= 142.8687 noot= 75.5 24-root 2 freq= 144.7273 38-root 3 freq= 144.949 noot= 76 24-root 2 freq= 146.8324 38-root 3 freq= 147.0595 noot= 76.5 24-root 2 freq= 148.9681 38-root 3 freq= 149.2007 noot= 77 24-root 2 freq= 151.1349 38-root 3 freq= 151.3732 noot= 77.5 24-root 2 freq= 153.3332 38-root 3 freq= 153.5772 noot= 78 24-root 2 freq= 155.5635 38-root 3 freq= 155.8134 noot= 78.5 24-root 2 freq= 157.8262 38-root 3 freq= 158.0821 noot= 79 24-root 2 freq= 160.1219 38-root 3 freq= 160.3838 noot= 79.5 24-root 2 freq= 162.4509 38-root 3 freq= 162.719 noot= 80 24-root 2 freq= 164.8138 38-root 3 freq= 165.0883 noot= 80.5 24-root 2 freq= 167.2111 38-root 3 freq= 167.4921 noot= 81 24-root 2 freq= 169.6432 38-root 3 freq= 169.9308 noot= 81.5 24-root 2 freq= 172.1107 38-root 3 freq= 172.4051 noot= 82 24-root 2 freq= 174.6142 38-root 3 freq= 174.9154 noot= 82.5 24-root 2 freq= 177.154 38-root 3 freq= 177.4622 noot= 83 24-root 2 freq= 179.7307 38-root 3 freq= 180.0461 noot= 83.5 24-root 2 freq= 182.345 38-root 3 freq= 182.6677
noot= 36 24-root 2 freq= 46.24931 38-root 3 freq= 46.26581 noot= 36.5 24-root 2 freq= 46.92202 38-root 3 freq= 46.93946 noot= 37 24-root 2 freq= 47.60452 38-root 3 freq= 47.62291 noot= 37.5 24-root 2 freq= 48.29694 38-root 3 freq= 48.31632 noot= 38 24-root 2 freq= 48.99944 38-root 3 freq= 49.01983 noot= 38.5 24-root 2 freq= 49.71215 38-root 3 freq= 49.73358 noot= 39 24-root 2 freq= 50.43523 38-root 3 freq= 50.45772 noot= 39.5 24-root 2 freq= 51.16883 38-root 3 freq= 51.1924 noot= 40 24-root 2 freq= 51.9131 38-root 3 freq= 51.93779 noot= 40.5 24-root 2 freq= 52.66819 38-root 3 freq= 52.69402 noot= 41 24-root 2 freq= 53.43426 38-root 3 freq= 53.46126 noot= 41.5 24-root 2 freq= 54.21149 38-root 3 freq= 54.23968 noot= 42 24-root 2 freq= 55.00001 38-root 3 freq= 55.02944 noot= 42.5 24-root 2 freq= 55.8 38-root 3 freq= 55.83069 noot= 43 24-root 2 freq= 56.61163 38-root 3 freq= 56.64361 noot= 43.5 24-root 2 freq= 57.43507 38-root 3 freq= 57.46836 noot= 44 24-root 2 freq= 58.27048 38-root 3 freq= 58.30512 noot= 44.5 24-root 2 freq= 59.11804 38-root 3 freq= 59.15407 noot= 45 24-root 2 freq= 59.97794 38-root 3 freq= 60.01538 noot= 45.5 24-root 2 freq= 60.85033 38-root 3 freq= 60.88922 noot= 46 24-root 2 freq= 61.73542 38-root 3 freq= 61.7758 noot= 46.5 24-root 2 freq= 62.63338 38-root 3 freq= 62.67528 noot= 47 24-root 2 freq= 63.54441 38-root 3 freq= 63.58786 noot= 47.5 24-root 2 freq= 64.46868 38-root 3 freq= 64.51372	noot= 84 24-root 2 freq= 184.9972 38-root 3 freq= 185.3274 noot= 84.5 24-root 2 freq= 187.6881 38-root 3 freq= 188.0258 noot= 85 24-root 2 freq= 190.4181 38-root 3 freq= 190.7636 noot= 85.5 24-root 2 freq= 193.1878 38-root 3 freq= 193.5412 noot= 86 24-root 2 freq= 195.9978 38-root 3 freq= 196.3592 noot= 86.5 24-root 2 freq= 198.8486 38-root 3 freq= 199.2183 noot= 87 24-root 2 freq= 201.7409 38-root 3 freq= 202.119 noot= 87.5 24-root 2 freq= 204.6753 38-root 3 freq= 205.0619 noot= 88 24-root 2 freq= 207.6524 38-root 3 freq= 208.0477 noot= 88.5 24-root 2 freq= 210.6728 38-root 3 freq= 211.077 noot= 89 24-root 2 freq= 213.7371 38-root 3 freq= 214.1503 noot= 89.5 24-root 2 freq= 216.8459 38-root 3 freq= 217.2684 noot= 90 24-root 2 freq= 220 38-root 3 freq= 220.432 noot= 90.5 24-root 2 freq= 223.2 38-root 3 freq= 223.6415 noot= 91 24-root 2 freq= 226.4465 38-root 3 freq= 226.8978 noot= 91.5 24-root 2 freq= 229.7403 38-root 3 freq= 230.2016 noot= 92 24-root 2 freq= 233.0819 38-root 3 freq= 233.5534 noot= 92.5 24-root 2 freq= 236.4722 38-root 3 freq= 236.954 noot= 93 24-root 2 freq= 239.9117 38-root 3 freq= 240.4042 noot= 93.5 24-root 2 freq= 243.4013 38-root 3 freq= 243.9046 noot= 94 24-root 2 freq= 246.9417 38-root 3 freq= 247.4559 noot= 94.5 24-root 2 freq= 250.5335 38-root 3 freq= 251.059 noot= 95 24-root 2 freq= 254.1776 38-root 3 freq= 254.7145 noot= 95.5 24-root 2 freq= 257.8747 38-root 3 freq= 258.4232
noot= 48 24-root 2 freq= 65.4064 38-root 3 freq= 65.45307 noot= 48.5 24-root 2 freq= 66.35776 38-root 3 freq= 66.40609 noot= 49 24-root 2 freq= 67.32296 38-root 3 freq= 67.37299 noot= 49.5 24-root 2 freq= 68.30219 38-root 3 freq= 68.35397 noot= 50 24-root 2 freq= 69.29567 38-root 3 freq= 69.34923 noot= 50.5 24-root 2 freq= 70.3036 38-root 3 freq= 70.35898 noot= 51 24-root 2 freq= 71.32619 38-root 3 freq= 71.38344 noot= 51.5 24-root 2 freq= 72.36365 38-root 3 freq= 72.42281 noot= 52 24-root 2 freq= 73.41621 38-root 3 freq= 73.47732 noot= 52.5 24-root 2 freq= 74.48407 38-root 3 freq= 74.54718 noot= 53 24-root 2 freq= 75.56747 38-root 3 freq= 75.63261 noot= 53.5 24-root 2 freq= 76.66662 38-root 3 freq= 76.73386 noot= 54 24-root 2 freq= 77.78176 38-root 3 freq= 77.85114 noot= 54.5 24-root 2 freq= 78.91312 38-root 3 freq= 78.98468 noot= 55 24-root 2 freq= 80.06094 38-root 3 freq= 80.13473 noot= 55.5 24-root 2 freq= 81.22545 38-root 3 freq= 81.30152 noot= 56 24-root 2 freq= 82.40691 38-root 3 freq= 82.4853 noot= 56.5 24-root 2 freq= 83.60554 38-root 3 freq= 83.68632 noot= 57 24-root 2 freq= 84.82161 38-root 3 freq= 84.90483 noot= 57.5 24-root 2 freq= 86.05537 38-root 3 freq= 86.14108 noot= 58 24-root 2 freq= 87.30708 38-root 3 freq= 87.39533 noot= 58.5 24-root 2 freq= 88.57698 38-root 3 freq= 88.66785 noot= 59 24-root 2 freq= 89.86536 38-root 3 freq= 89.95888 noot= 59.5 24-root 2 freq= 91.17248 38-root 3 freq= 91.26872	noot= 96 24-root 2 freq= 261.6256 38-root 3 freq= 262.186 noot= 96.5 24-root 2 freq= 265.431 38-root 3 freq= 266.0035 noot= 97 24-root 2 freq= 269.2918 38-root 3 freq= 269.8766 noot= 97.5 24-root 2 freq= 273.2088 38-root 3 freq= 273.8062 noot= 98 24-root 2 freq= 277.1827 38-root 3 freq= 277.7929 noot= 98.5 24-root 2 freq= 281.2144 38-root 3 freq= 281.8377 noot= 99 24-root 2 freq= 285.3047 38-root 3 freq= 285.9413 noot= 99.5 24-root 2 freq= 289.4546 38-root 3 freq= 290.1048 noot= 100 24-root 2 freq= 293.6648 38-root 3 freq= 294.3288 noot= 100.5 24-root 2 freq= 297.9363 38-root 3 freq= 298.6143 noot= 101 24-root 2 freq= 302.2699 38-root 3 freq= 302.9623 noot= 101.5 24-root 2 freq= 306.6665 38-root 3 freq= 307.3736 noot= 102 24-root 2 freq= 311.127 38-root 3 freq= 311.8491 noot= 102.5 24-root 2 freq= 315.6525 38-root 3 freq= 316.3897 noot= 103 24-root 2 freq= 320.2437 38-root 3 freq= 320.9964 noot= 103.5 24-root 2 freq= 324.9018 38-root 3 freq= 325.6703 noot= 104 24-root 2 freq= 329.6276 38-root 3 freq= 330.4122 noot= 104.5 24-root 2 freq= 334.4221 38-root 3 freq= 335.2231 noot= 105 24-root 2 freq= 339.2864 38-root 3 freq= 340.1041 noot= 105.5 24-root 2 freq= 344.2215 38-root 3 freq= 345.0562 noot= 106 24-root 2 freq= 349.2283 38-root 3 freq= 350.0803 noot= 106.5 24-root 2 freq= 354.3079 38-root 3 freq= 355.1776 noot= 107 24-root 2 freq= 359.4614 38-root 3 freq= 360.3492 noot= 107.5 24-root 2 freq= 364.6899 38-root 3 freq= 365.596
noot= 60 24-root 2 freq= 92.49862 38-root 3 freq= 92.59763 noot= 60.5 24-root 2 freq= 93.84405 38-root 3 freq= 93.94589 noot= 61 24-root 2 freq= 95.20904 38-root 3 freq= 95.31378 noot= 61.5 24-root 2 freq= 96.59389 38-root 3 freq= 96.70159 noot= 62 24-root 2 freq= 97.99888 38-root 3 freq= 98.1096 noot= 62.5 24-root 2 freq= 99.4243 38-root 3 freq= 99.53812 noot= 63 24-root 2 freq= 100.8705 38-root 3 freq= 100.9874 noot= 63.5 24-root 2 freq= 102.3376 38-root 3 freq= 102.4578 noot= 64 24-root 2 freq= 103.8262 38-root 3 freq= 103.9497 noot= 64.5 24-root 2 freq= 105.3364 38-root 3 freq= 105.4632 noot= 65 24-root 2 freq= 106.8685 38-root 3 freq= 106.9988 noot= 65.5 24-root 2 freq= 108.423 38-root 3 freq= 108.5568 noot= 66 24-root 2 freq= 110 38-root 3 freq= 110.1374 noot= 66.5 24-root 2 freq= 111.6 38-root 3 freq= 111.741 noot= 67 24-root 2 freq= 113.2233 38-root 3 freq= 113.368 noot= 67.5 24-root 2 freq= 114.8701 38-root 3 freq= 115.0187 noot= 68 24-root 2 freq= 116.541 38-root 3 freq= 116.6934 noot= 68.5 24-root 2 freq= 118.2361 38-root 3 freq= 118.3925 noot= 69 24-root 2 freq= 119.9559 38-root 3 freq= 120.1164 noot= 69.5 24-root 2 freq= 121.7007 38-root 3 freq= 121.8653 noot= 70 24-root 2 freq= 123.4708 38-root 3 freq= 123.6397 noot= 70.5 24-root 2 freq= 125.2668 38-root 3 freq= 125.44 noot= 71 24-root 2 freq= 127.0888 38-root 3 freq= 127.2664 noot= 71.5 24-root 2 freq= 128.9374 38-root 3 freq= 129.1195	noot= 108 24-root 2 freq= 369.9945 38-root 3 freq= 370.9192 noot= 108.5 24-root 2 freq= 375.3762 38-root 3 freq= 376.32 noot= 109 24-root 2 freq= 380.8362 38-root 3 freq= 381.7993 noot= 109.5 24-root 2 freq= 386.3755 38-root 3 freq= 387.3585 noot= 110 24-root 2 freq= 391.9955 38-root 3 freq= 392.9986 noot= 110.5 24-root 2 freq= 397.6972 38-root 3 freq= 398.7208 noot= 111 24-root 2 freq= 403.4818 38-root 3 freq= 404.5264 noot= 111.5 24-root 2 freq= 409.3506 38-root 3 freq= 410.4164 noot= 112 24-root 2 freq= 415.3048 38-root 3 freq= 416.3923 noot= 112.5 24-root 2 freq= 421.3455 38-root 3 freq= 422.4551 noot= 113 24-root 2 freq= 427.4741 38-root 3 freq= 428.6062 noot= 113.5 24-root 2 freq= 433.6919 38-root 3 freq= 434.8469 noot= 114 24-root 2 freq= 440.0001 38-root 3 freq= 441.1784 noot= 114.5 24-root 2 freq= 446.4 38-root 3 freq= 447.6022 noot= 115 24-root 2 freq= 452.8931 38-root 3 freq= 454.1195 noot= 115.5 24-root 2 freq= 459.4805 38-root 3 freq= 460.7316 noot= 116 24-root 2 freq= 466.1638 38-root 3 freq= 467.4401 noot= 116.5 24-root 2 freq= 472.9443 38-root 3 freq= 474.2462 noot= 117 24-root 2 freq= 479.8235 38-root 3 freq= 481.1514 noot= 117.5 24-root 2 freq= 486.8027 38-root 3 freq= 488.1572 noot= 118 24-root 2 freq= 493.8834 38-root 3 freq= 495.2649 noot= 118.5 24-root 2 freq= 501.0671 38-root 3 freq= 502.4762 noot= 119 24-root 2 freq= 508.3553 38-root 3 freq= 509.7924 noot= 119.5 24-root 2 freq= 515.7494 38-root 3 freq= 517.2153 noot= 120 24-root 2 freq= 523.2512 38-root 3 freq= 524.7461

Kwarttoonskwintencirkels in gelijkzwevende stemmingen:

in kwinten van 13 kwarttonen (te kleine kwinten, gelegen tussen de tritonus en de gelijkzwevende kwint):

 13                60.00
 2                 66.50
 15                61.00
 4                 67.50
 17                62.00
 6                 68.50
 19                63.00
 8                 69.50
 21                64.00
 10                70.50
 23                65.00
 12                71.50
 1                 66.00
 14                60.50
 3                 67.00
 16                61.50
 5                 68.00
 18                62.50
 7                 69.00
 20                63.50
 9                 70.00
 22                64.50
 11                71.00
 0                 65.50

Hiermee kunnen we 24 kwarttonen bereiken en de gehele cirkel doorlopen. Alleen in een harmonie die deze kwinten gebruikt kan doorheen het hele toonsysteem gemoduleerd worden. Deze kwinten zijn evenwel niet bepaald konsonant te noemen. Niettemin is het kompositorisch een erg interessant systeem omdat het diverse stelsels van funktionele harmonie mogelijk maakt.

In kwinten van 15 kwarttonen (te grote kwinten):

 15                60.00
 6                 67.50
 21                63.00
 12                70.50
 3                 66.00
 18                61.50
 9                 69.00
 0                 64.50

Hiermee kunnen we 8 kwarttonen bereiken. Met zulke kwinten bestaan er binnen het kwarttoonssysteem 3 verschillende sluitende kwintencirkels. Binnen elk kwintencirkelsysteem kunnen 8 andere intervallen bereikt worden, maar het is niet mogelijk van de ene cirkel naar een van de andere te moduleren met gebruikelijke muzikale technieken. Het naast elkaar bestaan van drie verschillende harmonische werelden, is op zich ook wel een muzikaal gegeven dat heel wat kreatieve en originele mogelijkheden schept.

in juiste reine kwinten:
 0       60.00               60.00
 1       67.02               67.00
 2       62.04               62.00
 3       69.06               69.00
 4       64.08               64.00
 5       71.10               71.00
 6       66.12               66.00
 7       61.14               61.00
 8       68.16               68.00
 9       63.18               63.00
 10      70.20               70.00
 11      65.22               65.00
 12      60.23               60.00
 13      67.25               67.50
 14      62.27               62.50
 15      69.29               69.50
 16      64.31               64.50
 17      71.33               71.50
 18      66.35               66.50
 19      61.37               61.50
 20      68.39               68.50
 21      63.41               63.50
 22      70.43               70.50
 23      65.45               65.50
 24      60.47               60.50
 25      67.49               67.50
 26      62.51               62.50
 27      69.53               69.50
 28      64.55               64.50
 29      71.57               71.50
 30      66.59               66.50
 31      61.61               61.50
 32      68.63               68.50
 33      63.65               63.50
 34      70.66               70.50
 35      65.68               65.50
 36      60.70               60.50
 37      67.72               67.50
 38      62.74               62.50
 39      69.76               70.00
 40      64.78               65.00
 41      71.80               72.00
 42      66.82               67.00
 43      61.84               62.00
 44      68.86               69.00
 45      63.88               64.00
 46      70.90               71.00
 47      65.92               66.00
 48      60.94               61.00
 49      67.96               68.00
 50      62.98               63.00
 51      70.00               70.00
 52      65.02               65.00
 53      60.04               60.00

aantal noten: 53

In het gewone kwarttoonssysteem bestaan naast elkaar twee onafhankelijke kwintencirkels. Het is niet mogelijk van het ene systeem naar het andere te moduleren via kwinten. Op grond daarvan maken heel wat van de harmonische systemen voor kwarttoonsmuziek dan ook eerder gebruik van de tweemaal grotere differentiemogelijkheden van de tertsen, met behoud van de 'traditionele' kwinten. Alleen mits een 53-toons systeem (zoals hierboven aangetoond en berekend, en eerder in deze uiteenzetting bekommentarieerd), sluit de kwintencirkel zich doorheen alle 24 kwarttonen.

Alle systemen die halve tonen verder onderverdelen, zijn verenigbaar met de traditionele westerse muziek. We vermelden daarvan alleen de verdeling in zesde-tonen (dit is de stemming waarin de cellist Franklin Cox zich bekwaamde). We zien onmiddellijk dat dergelijke oktaafverdeling geen voordelen oplevert op het vlak van platonische juistheid der intervallen. Ze is gewoon kwazi identisch met die van de gewone gelijkzwevende stemming..

Zesde-toonssysteem: halve toon bestaat uit 3 stappen, dus 36 onderverdelingen per oktaaf: 

Juistheid van de 6:5 kleine terts in cent:  15.64  2 ^ ( 9/ 36). Interval: 60   63
Juistheid van de 5:4 grote terts in cent: -13.69  2 ^ ( 12/ 36). Interval: 60   64
Juistheid van de 4:3 kwart in cent:-1.95  2 ^ ( 15/ 36). Interval: 60   65
Juistheid van de 3:2 kwint in cent:  1.96  2 ^ ( 21/ 36). Interval: 60   67

Achtste tonen werden alleen, wellicht eerder als konceptueel begrip, door sommige komponisten toegepast. Een kompositorisch, laat staan harmonisch systeem, werd uitgaande van een dergelijke granulatie bij ons weten nooit ontwikkeld.

Achtste toonsysteem: 48 onderverdelingen per oktaaf:

Juistheid van de 6:5 kleine terts in cent: -9.36  2 ^ ( 13/ 48). Interval: 60   63.25
Juistheid van de 5:4 grote terts in cent:  11.31  2 ^ ( 15/ 48). Interval: 60   63.75
Juistheid van de 4:3 kwart in cent:-1.95  2 ^ ( 20/ 48). Interval: 60   65
Juistheid van de 3:2 kwint in cent:  1.96  2 ^ ( 28/ 48). Interval: 60   67

We merken op dat de kwinten er bij verdere redelijke verdelingen niet beter op worden. Alleen bij de tertsen is er een merkbare verbetering naarmate de verdeling groter wordt. De differentiatie van de verschillende mogelijke tertsen neemt uiteraard sterk toe.

tabellen met de afwijkingen tegenover de juiste boventoonsstemming van alle gelijkzwevende stemmingen opgebouwd uit 7 tot 53 intervallen per oktaaf:

Gelijkzwevende verdelingen van het oktaaf

Overzicht over de juistheid van de basisintervallen in diverse getemperde stemmmingen afgemeten aan de geidealiseerde intervallen uit de majeur en mineur juiste boventoonsladders. De intervallen zijn uitgedrukt in halve tonen, de fout in cent.

De tabel is opgesteld voor diverse onderverdelingen van het oktaaf (root=2). Betekenis van de referentie interval waarden:

        2 = juiste boventoons seconde (9:8)
        3 = juiste boventoons kleine  terts (6:5)
        4 = juiste boventoons grote terts (5:4)
        5 = juiste boventoons kwart (rein) (4:3)
        7 = juiste bovenstoons kwint (rein) (3:2)
        8 = juiste boventoons mineur sixt (8:5)
        9 = juiste boventoons majeur sixt (5:3)
        10 = juiste boventoons mineur kleine septiem (9:5)
        11 = juiste boventoons majeur grote septiem (15:8)
        12 = juiste boventoons oktaaf (2:1)

Root: 2 Aantal verdelingen: 7 interval: 2 fout: 32.48 interval: 3 fout:-27.22 interval: 4 fout: 43.46 interval: 5 fout:-16.24 interval: 7 fout: 16.24 interval: 8 fout:-43.46 interval: 9 fout: 27.22 interval: 10 fout:-10.97 interval: 11 fout: 59.7 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 30 interval: 2 fout: 3.91 interval: 3 fout:-4.36 interval: 4 fout:-13.69 interval: 5 fout: 18.05 interval: 7 fout:-18.05 interval: 8 fout: 13.69 interval: 9 fout: 4.36 interval: 10 fout: 17.6 interval: 11 fout: 8.27 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 8 interval: 2 fout: 53.91 interval: 3 fout: 15.64 interval: 4 fout:-63.69 interval: 5 fout: 48.05 interval: 7 fout:-48.04 interval: 8 fout: 63.69 interval: 9 fout:-15.64 interval: 10 fout:-32.4 interval: 11 fout: 38.27 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 31 interval: 2 fout: 10.36 interval: 3 fout: 5.96 interval: 4 fout:-.78 interval: 5 fout:-5.18 interval: 7 fout: 5.18 interval: 8 fout: .78 interval: 9 fout:-5.96 interval: 10 fout: 11.14 interval: 11 fout: 4.4 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 9 interval: 2 fout:-62.76 interval: 3 fout: 48.97 interval: 4 fout:-13.69 interval: 5 fout:-35.29 interval: 7 fout: 35.29 interval: 8 fout: 13.69 interval: 9 fout:-48.97 interval: 10 fout:-49.07 interval: 11 fout: 21.6 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 32 interval: 2 fout: 16.41 interval: 3 fout: 15.64 interval: 4 fout: 11.31 interval: 5 fout: 10.55 interval: 7 fout:-10.54 interval: 8 fout:-11.31 interval: 9 fout:-15.64 interval: 10 fout: 5.1 interval: 11 fout: .77 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 10 interval: 2 fout:-36.09 interval: 3 fout:-44.36 interval: 4 fout: 26.31 interval: 5 fout: 18.05 interval: 7 fout:-18.05 interval: 8 fout:-26.31 interval: 9 fout: 44.36 interval: 10 fout: 57.6 interval: 11 fout: 8.27 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 33 interval: 2 fout:-14.27 interval: 3 fout:-11.63 interval: 4 fout:-13.69 interval: 5 fout:-11.05 interval: 7 fout: 11.05 interval: 8 fout: 13.69 interval: 9 fout: 11.63 interval: 10 fout:-.59 interval: 11 fout:-2.64 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 11 interval: 2 fout:-14.27 interval: 3 fout:-11.63 interval: 4 fout:-50.05 interval: 5 fout:-47.41 interval: 7 fout: 47.41 interval: 8 fout: 50.05 interval: 9 fout: 11.63 interval: 10 fout: 35.78 interval: 11 fout:-2.64 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 34 interval: 2 fout:-7.85 interval: 3 fout:-2.01 interval: 4 fout:-1.92 interval: 5 fout: 3.93 interval: 7 fout:-3.93 interval: 8 fout: 1.92 interval: 9 fout: 2.01 interval: 10 fout:-5.93 interval: 11 fout:-5.85 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 12 [dit is de gewone verdeling] interval: 2 fout: 3.91 interval: 3 fout: 15.64 interval: 4 fout:-13.69 interval: 5 fout:-1.95 interval: 7 fout: 1.96 interval: 8 fout: 13.69 interval: 9 fout:-15.64 interval: 10 fout: 17.6 interval: 11 fout:-11.73 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 35 interval: 2 fout:-1.8 interval: 3 fout: 7.07 interval: 4 fout: 9.17 interval: 5 fout:-16.24 interval: 7 fout: 16.24 interval: 8 fout:-9.17 interval: 9 fout:-7.07 interval: 10 fout:-10.97 interval: 11 fout:-8.87 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 13 interval: 2 fout: 19.29 interval: 3 fout: 38.72 interval: 4 fout: 17.08 interval: 5 fout: 36.51 interval: 7 fout:-36.51 interval: 8 fout:-17.08 interval: 9 fout:-38.72 interval: 10 fout: 2.21 interval: 11 fout:-19.42 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 36 interval: 2 fout: 3.91 interval: 3 fout: 15.64 interval: 4 fout:-13.69 interval: 5 fout:-1.95 interval: 7 fout: 1.96 interval: 8 fout: 13.69 interval: 9 fout:-15.64 interval: 10 fout:-15.74 interval: 11 fout:-11.73 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 14 interval: 2 fout: 32.48 interval: 3 fout:-27.22 interval: 4 fout:-42.26 interval: 5 fout:-16.24 interval: 7 fout: 16.24 interval: 8 fout: 42.26 interval: 9 fout: 27.22 interval: 10 fout:-10.97 interval: 11 fout:-26.02 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 37 interval: 2 fout: 9.32 interval: 3 fout:-8.68 interval: 4 fout:-2.88 interval: 5 fout: 11.56 interval: 7 fout:-11.56 interval: 8 fout: 2.88 interval: 9 fout: 8.68 interval: 10 fout: 12.19 interval: 11 fout:-14.43 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 15 interval: 2 fout:-36.09 interval: 3 fout:-4.36 interval: 4 fout:-13.69 interval: 5 fout: 18.05 interval: 7 fout:-18.05 interval: 8 fout: 13.69 interval: 9 fout: 4.36 interval: 10 fout:-22.4 interval: 11 fout:-31.73 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 38 interval: 2 fout: 14.44 interval: 3 fout:-.15 interval: 4 fout: 7.37 interval: 5 fout:-7.22 interval: 7 fout: 7.22 interval: 8 fout:-7.37 interval: 9 fout: .15 interval: 10 fout: 7.07 interval: 11 fout: 14.58 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 16 interval: 2 fout:-21.09 interval: 3 fout: 15.64 interval: 4 fout: 11.31 interval: 5 fout:-26.95 interval: 7 fout: 26.96 interval: 8 fout:-11.31 interval: 9 fout:-15.64 interval: 10 fout:-32.4 interval: 11 fout:-36.73 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 39 interval: 2 fout:-11.47 interval: 3 fout: 7.95 interval: 4 fout:-13.69 interval: 5 fout: 5.74 interval: 7 fout:-5.74 interval: 8 fout: 13.69 interval: 9 fout:-7.95 interval: 10 fout: 2.21 interval: 11 fout: 11.35 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 17 interval: 2 fout:-7.85 interval: 3 fout: 33.29 interval: 4 fout: 33.37 interval: 5 fout: 3.93 interval: 7 fout:-3.93 interval: 8 fout:-33.37 interval: 9 fout:-33.29 interval: 10 fout: 29.36 interval: 11 fout: 29.45 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 40 interval: 2 fout:-6.09 interval: 3 fout:-14.36 interval: 4 fout:-3.69 interval: 5 fout:-11.95 interval: 7 fout: 11.96 interval: 8 fout: 3.69 interval: 9 fout: 14.36 interval: 10 fout:-2.4 interval: 11 fout: 8.27 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 18 interval: 2 fout: 3.91 interval: 3 fout:-17.69 interval: 4 fout:-13.69 interval: 5 fout: 31.38 interval: 7 fout:-31.38 interval: 8 fout: 13.69 interval: 9 fout: 17.69 interval: 10 fout: 17.6 interval: 11 fout: 21.6 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 41 interval: 2 fout:-.97 interval: 3 fout:-6.31 interval: 4 fout: 5.83 interval: 5 fout: .48 interval: 7 fout:-.48 interval: 8 fout:-5.83 interval: 9 fout: 6.31 interval: 10 fout:-6.79 interval: 11 fout: 5.34 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 19 interval: 2 fout: 14.44 interval: 3 fout:-.15 interval: 4 fout: 7.37 interval: 5 fout:-7.22 interval: 7 fout: 7.22 interval: 8 fout:-7.37 interval: 9 fout: .15 interval: 10 fout: 7.07 interval: 11 fout: 14.58 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 42 interval: 2 fout: 3.91 interval: 3 fout: 1.36 interval: 4 fout:-13.69 interval: 5 fout: 12.33 interval: 7 fout:-12.33 interval: 8 fout: 13.69 interval: 9 fout:-1.36 interval: 10 fout:-10.97 interval: 11 fout: 2.55 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 20 interval: 2 fout: 23.91 interval: 3 fout: 15.64 interval: 4 fout: 26.31 interval: 5 fout: 18.05 interval: 7 fout:-18.05 interval: 8 fout:-26.31 interval: 9 fout:-15.64 interval: 10 fout:-2.4 interval: 11 fout: 8.27 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 43 interval: 2 fout: 8.56 interval: 3 fout: 8.66 interval: 4 fout:-4.38 interval: 5 fout:-4.28 interval: 7 fout: 4.28 interval: 8 fout: 4.38 interval: 9 fout:-8.66 interval: 10 fout: 12.94 interval: 11 fout:-.1 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 21 interval: 2 fout:-24.66 interval: 3 fout:-27.22 interval: 4 fout:-13.69 interval: 5 fout:-16.24 interval: 7 fout: 16.24 interval: 8 fout: 13.69 interval: 9 fout: 27.22 interval: 10 fout:-10.97 interval: 11 fout: 2.55 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 44 interval: 2 fout: 13 interval: 3 fout:-11.63 interval: 4 fout: 4.5 interval: 5 fout: 7.14 interval: 7 fout:-7.14 interval: 8 fout:-4.5 interval: 9 fout: 11.63 interval: 10 fout: 8.51 interval: 11 fout:-2.64 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 22 interval: 2 fout:-14.27 interval: 3 fout:-11.63 interval: 4 fout: 4.5 interval: 5 fout: 7.14 interval: 7 fout:-7.14 interval: 8 fout:-4.5 interval: 9 fout: 11.63 interval: 10 fout:-18.77 interval: 11 fout:-2.64 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 45 interval: 2 fout:-9.42 interval: 3 fout:-4.36 interval: 4 fout: 12.98 interval: 5 fout:-8.62 interval: 7 fout: 8.62 interval: 8 fout:-12.98 interval: 9 fout: 4.36 interval: 10 fout: 4.26 interval: 11 fout:-5.06 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 23 interval: 2 fout:-4.79 interval: 3 fout: 2.6 interval: 4 fout: 21.1 interval: 5 fout:-23.69 interval: 7 fout: 23.69 interval: 8 fout:-21.1 interval: 9 fout:-2.6 interval: 10 fout:-25.88 interval: 11 fout:-7.38 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 46 interval: 2 fout:-4.79 interval: 3 fout: 2.6 interval: 4 fout:-4.99 interval: 5 fout: 2.39 interval: 7 fout:-2.39 interval: 8 fout: 4.99 interval: 9 fout:-2.6 interval: 10 fout: .21 interval: 11 fout:-7.38 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 24 interval: 2 fout: 3.91 interval: 3 fout: 15.64 interval: 4 fout:-13.69 interval: 5 fout:-1.95 interval: 7 fout: 1.96 interval: 8 fout: 13.69 interval: 9 fout:-15.64 interval: 10 fout: 17.6 interval: 11 fout:-11.73 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 47 interval: 2 fout:-.35 interval: 3 fout: 9.26 interval: 4 fout: 3.34 interval: 5 fout:-12.59 interval: 7 fout: 12.59 interval: 8 fout:-3.33 interval: 9 fout:-9.26 interval: 10 fout:-3.68 interval: 11 fout:-9.6 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 25 interval: 2 fout: 11.91 interval: 3 fout:-20.36 interval: 4 fout: 2.31 interval: 5 fout: 18.05 interval: 7 fout:-18.05 interval: 8 fout:-2.31 interval: 9 fout: 20.36 interval: 10 fout: 9.6 interval: 11 fout:-15.73 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 48 interval: 2 fout: 3.91 interval: 3 fout:-9.36 interval: 4 fout: 11.31 interval: 5 fout:-1.95 interval: 7 fout: 1.96 interval: 8 fout:-11.31 interval: 9 fout: 9.36 interval: 10 fout:-7.4 interval: 11 fout:-11.73 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 26 interval: 2 fout: 19.29 interval: 3 fout:-7.44 interval: 4 fout: 17.08 interval: 5 fout:-9.65 interval: 7 fout: 9.65 interval: 8 fout:-17.08 interval: 9 fout: 7.44 interval: 10 fout: 2.21 interval: 11 fout:-19.42 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 49 interval: 2 fout: 7.99 interval: 3 fout:-2.73 interval: 4 fout:-5.52 interval: 5 fout: 8.25 interval: 7 fout:-8.25 interval: 8 fout: 5.52 interval: 9 fout: 2.73 interval: 10 fout:-10.97 interval: 11 fout: 10.72 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 27 interval: 2 fout:-18.31 interval: 3 fout: 4.53 interval: 4 fout:-13.69 interval: 5 fout: 9.16 interval: 7 fout:-9.16 interval: 8 fout: 13.69 interval: 9 fout:-4.53 interval: 10 fout:-4.63 interval: 11 fout: 21.6 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 50 interval: 2 fout: 11.91 interval: 3 fout: 3.64 interval: 4 fout: 2.31 interval: 5 fout:-5.95 interval: 7 fout: 5.96 interval: 8 fout:-2.31 interval: 9 fout:-3.64 interval: 10 fout: 9.6 interval: 11 fout: 8.27 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 28 interval: 2 fout:-10.38 interval: 3 fout: 15.64 interval: 4 fout: .6 interval: 5 fout:-16.24 interval: 7 fout: 16.24 interval: 8 fout:-.6 interval: 9 fout:-15.64 interval: 10 fout:-10.97 interval: 11 fout: 16.84 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 51 interval: 2 fout:-7.85 interval: 3 fout: 9.76 interval: 4 fout: 9.84 interval: 5 fout: 3.93 interval: 7 fout:-3.93 interval: 8 fout:-9.84 interval: 9 fout:-9.76 interval: 10 fout: 5.83 interval: 11 fout: 5.92 interval: 12 fout: 0
Root: 2 Aantal verdelingen: 29 interval: 2 fout:-2.99 interval: 3 fout:-15.39 interval: 4 fout: 13.9 interval: 5 fout: 1.49 interval: 7 fout:-1.49 interval: 8 fout:-13.9 interval: 9 fout: 15.39 interval: 10 fout:-16.89 interval: 11 fout: 12.41 interval: 12 fout: 0	Root: 2 Aantal verdelingen: 52 interval: 2 fout:-3.78 interval: 3 fout:-7.44 interval: 4 fout:-5.99 interval: 5 fout:-9.65 interval: 7 fout: 9.65 interval: 8 fout: 5.99 interval: 9 fout: 7.44 interval: 10 fout: 2.21 interval: 11 fout: 3.65 interval: 12 fout: 0
	Root: 2 Aantal verdelingen: 53 interval: 2 fout: .14 interval: 3 fout:-1.34 interval: 4 fout: 1.41 interval: 5 fout:-.07 interval: 7 fout: .07 interval: 8 fout:-1.41 interval: 9 fout: 1.34 interval: 10 fout:-1.27 interval: 11 fout: 1.48 interval: 12 fout: 0

Gelijkzwevende verdelingen van de duodeciem

Overzicht over de juistheid van de basisintervallen in diverse getemperde stemmingen afgemeten aan de geidealiseerde intervallen uit de majeur en mineur juiste boventoonsladders. De intervallen zijn uitgedrukt in halve tonen, de fout in cent. De tabel is opgesteld voor diverse onderverdelingen van de duodeciem (root=3).

Betekenis van de referentie interval waarden:

        2 = juiste boventoons seconde (9:8)
        3 = juiste boventoons kleine  terts (6:5)
        4 = juiste boventoons grote terts (5:4)
        5 = juiste boventoons kwart (rein) (4:3)
        7 = juiste bovenstoons kwint (rein) (3:2)
        8 = juiste boventoons mineur sixt (8:5)
        9 = juiste boventoons majeur sixt (5:3)
        10 = juiste boventoons mineur kleine septiem (9:5)
        11 = juiste boventoons majeur grote septiem (15:8)
        12 = juiste boventoons oktaaf (2:1)

Root: 3 Aantal verdelingen: 7 interval: 2 fout:-67.8 interval: 3 fout: 43.93 interval: 4 fout: 114.61 interval: 5 fout:-45.37 interval: 7 fout:-113.17 interval: 8 fout:-1.44 interval: 9 fout: 69.24 interval: 10 fout:-69.24 interval: 11 fout: 1.44 interval: 12 fout: 113.17	Root: 3 Aantal verdelingen: 23 interval: 2 fout: 38.52 interval: 3 fout:-15.13 interval: 4 fout:-27.15 interval: 5 fout: 1.88 interval: 7 fout: 40.41 interval: 8 fout:-13.25 interval: 9 fout:-25.27 interval: 10 fout: 25.27 interval: 11 fout: 13.25 interval: 12 fout:-40.41	Root: 3 Aantal verdelingen: 39 interval: 2 fout: 8.84 interval: 3 fout: 23.03 interval: 4 fout:-3.83 interval: 5 fout: 10.36 interval: 7 fout: 19.2 interval: 8 fout:-15.37 interval: 9 fout: 6.53 interval: 10 fout:-6.53 interval: 11 fout: 15.37 interval: 12 fout:-19.2
Root: 3 Aantal verdelingen: 8 interval: 2 fout:-33.83 interval: 3 fout: 77.9 interval: 4 fout:-89.18 interval: 5 fout: 22.56 interval: 7 fout:-11.28 interval: 8 fout: 100.45 interval: 9 fout:-66.62 interval: 10 fout: 66.62 interval: 11 fout:-100.45 interval: 12 fout: 11.28	Root: 3 Aantal verdelingen: 24 interval: 2 fout:-33.83 interval: 3 fout:-1.35 interval: 4 fout:-9.93 interval: 5 fout: 22.56 interval: 7 fout:-11.28 interval: 8 fout: 21.21 interval: 9 fout: 12.63 interval: 10 fout:-12.63 interval: 11 fout:-21.21 interval: 12 fout: 11.28	Root: 3 Aantal verdelingen: 40 interval: 2 fout: 13.71 interval: 3 fout:-17.2 interval: 4 fout: 5.92 interval: 5 fout: 22.56 interval: 7 fout:-11.28 interval: 8 fout: 5.36 interval: 9 fout:-19.07 interval: 10 fout: 19.07 interval: 11 fout:-5.36 interval: 12 fout: 11.28
Root: 3 Aantal verdelingen: 9 interval: 2 fout:-7.42 interval: 3 fout: 104.31 interval: 4 fout:-36.34 interval: 5 fout: 75.39 interval: 7 fout: 67.97 interval: 8 fout:-31.63 interval: 9 fout: 39.05 interval: 10 fout:-39.05 interval: 11 fout: 31.63 interval: 12 fout:-67.97	Root: 3 Aantal verdelingen: 25 interval: 2 fout:-24.32 interval: 3 fout: 11.33 interval: 4 fout: 5.92 interval: 5 fout:-34.5 interval: 7 fout: 17.25 interval: 8 fout:-23.17 interval: 9 fout:-28.58 interval: 10 fout: 28.58 interval: 11 fout: 23.17 interval: 12 fout:-17.25	Root: 3 Aantal verdelingen: 41 interval: 2 fout: 18.35 interval: 3 fout:-9.08 interval: 4 fout: 15.2 interval: 5 fout:-12.24 interval: 7 fout: 6.12 interval: 8 fout:-21.32 interval: 9 fout: 2.96 interval: 10 fout:-2.96 interval: 11 fout: 21.32 interval: 12 fout:-6.12
Root: 3 Aantal verdelingen: 10 interval: 2 fout: 13.71 interval: 3 fout:-64.75 interval: 4 fout: 5.92 interval: 5 fout:-72.54 interval: 7 fout:-58.83 interval: 8 fout: 52.9 interval: 9 fout:-66.62 interval: 10 fout: 66.62 interval: 11 fout:-52.9 interval: 12 fout: 58.83	Root: 3 Aantal verdelingen: 26 interval: 2 fout:-15.55 interval: 3 fout: 23.03 interval: 4 fout: 20.55 interval: 5 fout:-14.02 interval: 7 fout:-29.57 interval: 8 fout: 9.01 interval: 9 fout: 6.53 interval: 10 fout:-6.53 interval: 11 fout:-9.01 interval: 12 fout: 29.57	Root: 3 Aantal verdelingen: 42 interval: 2 fout:-22.51 interval: 3 fout:-1.35 interval: 4 fout:-21.25 interval: 5 fout:-.09 interval: 7 fout:-22.6 interval: 8 fout:-1.44 interval: 9 fout:-21.33 interval: 10 fout: 21.33 interval: 11 fout: 1.44 interval: 12 fout: 22.6
Root: 3 Aantal verdelingen: 11 interval: 2 fout: 31 interval: 3 fout:-30.17 interval: 4 fout: 40.5 interval: 5 fout:-20.67 interval: 7 fout: 10.34 interval: 8 fout:-50.84 interval: 9 fout: 19.83 interval: 10 fout:-19.83 interval: 11 fout: 50.84 interval: 12 fout:-10.33	Root: 3 Aantal verdelingen: 27 interval: 2 fout:-7.42 interval: 3 fout: 33.87 interval: 4 fout: 34.1 interval: 5 fout: 4.95 interval: 7 fout:-2.47 interval: 8 fout:-31.63 interval: 9 fout:-31.4 interval: 10 fout: 31.4 interval: 11 fout: 31.63 interval: 12 fout: 2.47	Root: 3 Aantal verdelingen: 43 interval: 2 fout:-17.25 interval: 3 fout: 6.02 interval: 4 fout:-11.77 interval: 5 fout: 11.5 interval: 7 fout:-5.75 interval: 8 fout: 17.52 interval: 9 fout:-.27 interval: 10 fout: .27 interval: 11 fout:-17.52 interval: 12 fout: 5.75
Root: 3 Aantal verdelingen: 12 interval: 2 fout: 45.41 interval: 3 fout:-1.35 interval: 4 fout: 69.32 interval: 5 fout: 22.56 interval: 7 fout: 67.97 interval: 8 fout: 21.21 interval: 9 fout:-66.62 interval: 10 fout: 66.62 interval: 11 fout:-21.21 interval: 12 fout:-67.97	Root: 3 Aantal verdelingen: 28 interval: 2 fout: .13 interval: 3 fout:-23.99 interval: 4 fout:-21.25 interval: 5 fout: 22.56 interval: 7 fout: 22.69 interval: 8 fout:-1.44 interval: 9 fout: 1.31 interval: 10 fout:-1.31 interval: 11 fout: 1.44 interval: 12 fout:-22.69	Root: 3 Aantal verdelingen: 44 interval: 2 fout:-12.22 interval: 3 fout: 13.06 interval: 4 fout:-2.72 interval: 5 fout:-20.67 interval: 7 fout: 10.34 interval: 8 fout:-7.61 interval: 9 fout: 19.83 interval: 10 fout:-19.83 interval: 11 fout: 7.61 interval: 12 fout:-10.33
Root: 3 Aantal verdelingen: 13 interval: 2 fout: 57.61 interval: 3 fout: 23.03 interval: 4 fout:-52.6 interval: 5 fout: 59.13 interval: 7 fout:-29.57 interval: 8 fout:-64.14 interval: 9 fout: 6.53 interval: 10 fout:-6.53 interval: 11 fout: 64.14 interval: 12 fout: 29.57	Root: 3 Aantal verdelingen: 29 interval: 2 fout: 7.16 interval: 3 fout:-12.28 interval: 4 fout:-7.19 interval: 5 fout:-26.63 interval: 7 fout:-19.48 interval: 8 fout: 26.67 interval: 9 fout: 31.76 interval: 10 fout:-31.76 interval: 11 fout:-26.67 interval: 12 fout: 19.48	Root: 3 Aantal verdelingen: 45 interval: 2 fout:-7.42 interval: 3 fout: 19.78 interval: 4 fout: 5.92 interval: 5 fout:-9.14 interval: 7 fout:-16.56 interval: 8 fout: 10.64 interval: 9 fout:-3.22 interval: 10 fout: 3.22 interval: 11 fout:-10.64 interval: 12 fout: 16.56
Root: 3 Aantal verdelingen: 14 interval: 2 fout:-67.8 interval: 3 fout: 43.93 interval: 4 fout:-21.25 interval: 5 fout:-45.37 interval: 7 fout: 22.69 interval: 8 fout:-1.44 interval: 9 fout:-66.62 interval: 10 fout: 66.62 interval: 11 fout: 1.44 interval: 12 fout:-22.69	Root: 3 Aantal verdelingen: 30 interval: 2 fout: 13.71 interval: 3 fout:-1.35 interval: 4 fout: 5.92 interval: 5 fout:-9.14 interval: 7 fout: 4.57 interval: 8 fout:-10.49 interval: 9 fout:-3.22 interval: 10 fout: 3.22 interval: 11 fout: 10.49 interval: 12 fout:-4.57	Root: 3 Aantal verdelingen: 46 interval: 2 fout:-2.82 interval: 3 fout:-15.13 interval: 4 fout: 14.19 interval: 5 fout: 1.88 interval: 7 fout:-.94 interval: 8 fout:-13.25 interval: 9 fout: 16.08 interval: 10 fout:-16.08 interval: 11 fout: 13.25 interval: 12 fout: .94
Root: 3 Aantal verdelingen: 15 interval: 2 fout:-49.68 interval: 3 fout: 62.05 interval: 4 fout: 5.92 interval: 5 fout:-9.14 interval: 7 fout:-58.83 interval: 8 fout: 52.9 interval: 9 fout:-3.22 interval: 10 fout: 3.22 interval: 11 fout:-52.9 interval: 12 fout: 58.83	Root: 3 Aantal verdelingen: 31 interval: 2 fout: 19.85 interval: 3 fout: 8.87 interval: 4 fout: 18.19 interval: 5 fout: 7.22 interval: 7 fout: 27.07 interval: 8 fout: 16.09 interval: 9 fout: 25.41 interval: 10 fout:-25.41 interval: 11 fout:-16.09 interval: 12 fout:-27.07	Root: 3 Aantal verdelingen: 47 interval: 2 fout: 1.57 interval: 3 fout:-8.1 interval: 4 fout:-18.36 interval: 5 fout: 12.44 interval: 7 fout: 14.01 interval: 8 fout: 4.34 interval: 9 fout:-5.92 interval: 10 fout: 5.92 interval: 11 fout:-4.34 interval: 12 fout:-14.01
Root: 3 Aantal verdelingen: 16 interval: 2 fout:-33.83 interval: 3 fout:-40.98 interval: 4 fout: 29.7 interval: 5 fout: 22.56 interval: 7 fout:-11.28 interval: 8 fout:-18.42 interval: 9 fout: 52.25 interval: 10 fout:-52.25 interval: 11 fout: 18.42 interval: 12 fout: 11.28	Root: 3 Aantal verdelingen: 32 interval: 2 fout: 25.6 interval: 3 fout: 18.46 interval: 4 fout: 29.7 interval: 5 fout: 22.56 interval: 7 fout:-11.28 interval: 8 fout:-18.42 interval: 9 fout:-7.18 interval: 10 fout: 7.18 interval: 11 fout: 18.42 interval: 12 fout: 11.28	Root: 3 Aantal verdelingen: 48 interval: 2 fout: 5.79 interval: 3 fout:-1.35 interval: 4 fout:-9.93 interval: 5 fout:-17.07 interval: 7 fout:-11.28 interval: 8 fout:-18.42 interval: 9 fout: 12.63 interval: 10 fout:-12.63 interval: 11 fout: 18.42 interval: 12 fout: 11.28
Root: 3 Aantal verdelingen: 17 interval: 2 fout:-19.85 interval: 3 fout:-20 interval: 4 fout: 50.67 interval: 5 fout: 50.53 interval: 7 fout: 30.68 interval: 8 fout: 30.53 interval: 9 fout:-10.68 interval: 10 fout: 10.68 interval: 11 fout:-30.53 interval: 12 fout:-30.68	Root: 3 Aantal verdelingen: 33 interval: 2 fout:-26.63 interval: 3 fout: 27.47 interval: 4 fout:-17.13 interval: 5 fout:-20.67 interval: 7 fout: 10.34 interval: 8 fout: 6.8 interval: 9 fout: 19.83 interval: 10 fout:-19.83 interval: 11 fout:-6.8 interval: 12 fout:-10.33	Root: 3 Aantal verdelingen: 49 interval: 2 fout: 9.83 interval: 3 fout: 5.12 interval: 4 fout:-1.84 interval: 5 fout:-6.56 interval: 7 fout: 3.28 interval: 8 fout:-1.44 interval: 9 fout:-8.4 interval: 10 fout: 8.4 interval: 11 fout: 1.44 interval: 12 fout:-3.28
Root: 3 Aantal verdelingen: 18 interval: 2 fout:-7.42 interval: 3 fout:-1.35 interval: 4 fout:-36.34 interval: 5 fout:-30.28 interval: 7 fout:-37.69 interval: 8 fout:-31.63 interval: 9 fout: 39.05 interval: 10 fout:-39.05 interval: 11 fout: 31.63 interval: 12 fout: 37.69	Root: 3 Aantal verdelingen: 34 interval: 2 fout:-19.85 interval: 3 fout:-20 interval: 4 fout:-5.27 interval: 5 fout:-5.41 interval: 7 fout:-25.26 interval: 8 fout:-25.41 interval: 9 fout:-10.68 interval: 10 fout: 10.68 interval: 11 fout: 25.41 interval: 12 fout: 25.26	Root: 3 Aantal verdelingen: 50 interval: 2 fout: 13.71 interval: 3 fout: 11.33 interval: 4 fout: 5.92 interval: 5 fout: 3.54 interval: 7 fout: 17.25 interval: 8 fout: 14.87 interval: 9 fout: 9.46 interval: 10 fout:-9.46 interval: 11 fout:-14.87 interval: 12 fout:-17.25
Root: 3 Aantal verdelingen: 19 [dit is de kromatische toonladder die we kennen, maar dan gebaseerd op duodeciem temperament] interval: 2 fout: 3.7 interval: 3 fout: 15.33 interval: 4 fout:-14.1 interval: 5 fout:-2.47 interval: 7 fout: 1.24 interval: 8 fout: 12.86 interval: 9 fout:-16.57 interval: 10 fout: 16.57 interval: 11 fout:-12.86 interval: 12 fout:-1.24	Root: 3 Aantal verdelingen: 35 interval: 2 fout:-13.46 interval: 3 fout:-10.41 interval: 4 fout: 5.92 interval: 5 fout: 8.97 interval: 7 fout:-4.49 interval: 8 fout:-1.44 interval: 9 fout: 14.89 interval: 10 fout:-14.89 interval: 11 fout: 1.44 interval: 12 fout: 4.49	Root: 3 Aantal verdelingen: 51 interval: 2 fout: 17.44 interval: 3 fout: 17.3 interval: 4 fout: 13.38 interval: 5 fout: 13.23 interval: 7 fout:-6.62 interval: 8 fout:-6.76 interval: 9 fout:-10.68 interval: 10 fout: 10.68 interval: 11 fout: 6.76 interval: 12 fout: 6.62
Root: 3 Aantal verdelingen: 20 interval: 2 fout: 13.71 interval: 3 fout: 30.35 interval: 4 fout: 5.92 interval: 5 fout: 22.56 interval: 7 fout: 36.27 interval: 8 fout:-42.19 interval: 9 fout: 28.48 interval: 10 fout:-28.48 interval: 11 fout: 42.19 interval: 12 fout:-36.27	Root: 3 Aantal verdelingen: 36 interval: 2 fout:-7.42 interval: 3 fout:-1.35 interval: 4 fout: 16.49 interval: 5 fout: 22.56 interval: 7 fout: 15.14 interval: 8 fout: 21.21 interval: 9 fout:-13.79 interval: 10 fout: 13.79 interval: 11 fout:-21.21 interval: 12 fout:-15.14	Root: 3 Aantal verdelingen: 52 interval: 2 fout:-15.55 interval: 3 fout:-13.54 interval: 4 fout:-16.02 interval: 5 fout:-14.02 interval: 7 fout: 7.01 interval: 8 fout: 9.01 interval: 9 fout: 6.53 interval: 10 fout:-6.53 interval: 11 fout:-9.01 interval: 12 fout:-7.01
Root: 3 Aantal verdelingen: 21 interval: 2 fout: 22.77 interval: 3 fout: 43.93 interval: 4 fout: 24.04 interval: 5 fout: 45.2 interval: 7 fout:-22.6 interval: 8 fout:-1.44 interval: 9 fout:-21.33 interval: 10 fout: 21.33 interval: 11 fout: 1.44 interval: 12 fout: 22.6	Root: 3 Aantal verdelingen: 37 interval: 2 fout:-1.71 interval: 3 fout: 7.22 interval: 4 fout:-24.92 interval: 5 fout:-16 interval: 7 fout:-17.7 interval: 8 fout:-8.78 interval: 9 fout: 10.49 interval: 10 fout:-10.49 interval: 11 fout: 8.78 interval: 12 fout: 17.7	Root: 3 Aantal verdelingen: 53 interval: 2 fout:-11.41 interval: 3 fout:-7.33 interval: 4 fout:-8.43 interval: 5 fout:-4.36 interval: 7 fout:-15.76 interval: 8 fout:-11.69 interval: 9 fout:-12.79 interval: 10 fout: 12.79 interval: 11 fout: 11.69 interval: 12 fout: 15.76
Root: 3 Aantal verdelingen: 22 interval: 2 fout: 31 interval: 3 fout:-30.17 interval: 4 fout: 40.5 interval: 5 fout:-20.67 interval: 7 fout: 10.34 interval: 8 fout: 35.61 interval: 9 fout: 19.83 interval: 10 fout:-19.83 interval: 11 fout:-35.61 interval: 12 fout:-10.33	Root: 3 Aantal verdelingen: 38 interval: 2 fout: 3.7 interval: 3 fout: 15.33 interval: 4 fout:-14.1 interval: 5 fout:-2.47 interval: 7 fout: 1.24 interval: 8 fout: 12.86 interval: 9 fout:-16.57 interval: 10 fout: 16.57 interval: 11 fout:-12.86 interval: 12 fout:-1.24

Wie nog meer tabellen zelf wil uitrekenen stellen we graag de door ons voor dit doel ontwikkelde software ter beschikking.

NIET GELIJKZWEVENDE PLATONISCHE BOVENTOONSSTEMMINGEN

Alle hier uitgevoerde berekeningen gaan uit van diapason La = 440.0Hz. Noten worden uitgedrukt als fraktionele midi getallen, waarbij noot 60 overeenkomt met de centrale Do (C) op het pianoklavier en in het gelijkzwevend 12-toons getemperd systeem. De reeksen zijn berekend vanaf grondtoon Do (C=36).

Toonreeksen in oplopende harmonische verhoudingen: In de linkerkolom: de boventoonsratio (steeds een verhouding van twee gehele getallen), in de tweede het nootequivalent in fraktionele midi. Dubbels werden in de tabellen weggelaten. ( ½ = 2/4 = 4/8 enz....)

Alle niet gelijkzwevende stemmingen die op eenvoudige getalverhoudingen zijn gesteund, bestaan uit een selektie uit deze intervallen. Deze selekties kunnen diatonisch zijn (opgebouwd uit twee tetrakorden elk bestaande uit twee soorten intervallen zodat we uitkomen op 7 toontrappen per oktaaf), pentatonisch of kromatisch. Ook toonschalen met 19 en 31 tonen kunnen zo worden samengesteld.

Bij het maken van selekties uit de mogelijke 'juiste' tonen kunnen we enerzijds pogen zo weinig mogelijk verschillende intervallen te gebruiken, zoals bvb in de pythagereische toonschaal waarin slechts 2 intervallen voorkomen tussen opeenvolgende tonen in de schaal: 9:8 en 256/243. De ladder ziet eruit als:

1:1	9:8	81:64	4:3	3:2	27:16	243:128	2:1
36.00	38.04		40.98	43.02	45.06		48.00

Maar, afgezien van oktaaf en kwint, komt deze schaal eerder slecht overeen met 'juiste' boventonen. Daarvoor zijn de termen van de verhoudingsgetallen immers veel te groot. De terts bvb. 81:64 = 1.266 is heel wat hoger dan de overeenkomstige platonische harmoniek 5:4 = 1.25. Dit maakt de pythogoreische toonschaal eerder ongeschikt voor 'harmonie' hoewel ze op melodisch vlak heel redelijk klinkt. Een akkoord bestaande uit de Do-Mi terts levert immers ca. 16 zwevingen op. Dit valt audioperceptorisch gezien binnen de kritische bandbreedte om het als een dissonant waar te nemen. Het aantal zwevingen voor de bekende gelijkzwevende terts Do-Mi, in dezelfde ligging is slechts ca. 10.

Zarlino poogde in de zestiende eeuw een basis te vinden voor een muziek gebaseerd op de drie harmonische majeur drieklanken: tonika, subdominant, dominant. Hij stelde daarbij voor drie verhoudingen te gebruiken: 1, 5:4, 3:2. Zijn frekwentieverhoudingen komen er uit te zien als:

1:1	9:8	5:4	4:3	3:2	5:3	15:8	2:1
36.00	38.04	39.86	40.98	43.02	44.84	46.88	48.00

De genoemde drieklanken klinken in deze schaal bijzonder konsonant en zwevingsvrij, maar transpositie naar andere toonaarden wordt nu wel heel erg problematisch. De kwint Re-La levert ons nu immers niet minder dan 11 zwevingen op. Het Zarlino systeem kent drie kwalitatief verschillende intervallen: de halve toon met verhouding 16:5, en twee soorten hele tonen: 9:8 (do-re, fa-sol en la-si) en 10:9 (Si-Do, sol-la). Het verschil tussen deze beide hele tonen nml. (9/8)/(10/9) = 81/80 = 1.0125. Dit verschil is men de syntonische komma gaan noemen, ongeveer een negende van een toon. Die is verschillend maar numeriek in dezelfde grootteorde dan de pythagereische komma, die slaat op het niet sluiten van de eerste periode van de kwintenspiraal.

Een vrij gangbare selektie waarmee 12 toontrappen per oktaaf kunnen worden samengesteld wordt gedefinieerd alsvolgt:

1:1

15:14

10:9

6:5

5:4

4:3

10:7

3:2

5:3

32:19

12:7

15:8

In fractionele midi getallen -de cent afwijking tegenover de gelijkzwevende kromatische stemming is het gedeelte na de komma- levert dit volg plaatje op:

36.00

37.19

37.82

39.16

39.86

40.98

42.17

43.02

44.84

45.02

45.33

46.88

Een nogal uitgebreidde en in elk geval het gehele bereik van de gebruikelijke tessituur beslaande berekening van alle platonische intervalverhoudingen geven we hier:

1: 1 36

 2: 1          48
 3: 1          55.02
 3: 2          43.02
 4: 1          60
 4: 3          40.98
 5: 1          63.86
 5: 2          51.86
 5: 3          44.84
 5: 4          39.86
 6: 1          67.02
 6: 5          39.16
 7: 1          69.69
 7: 2          57.69
 7: 3          50.67
 7: 4          45.69
 7: 5          41.83
 7: 6          38.67
 8: 1          72

16: 3 64.98

 16: 5         56.14
 16: 7         50.31
 16: 9         45.96
 16: 11        42.49
 16: 13        39.59
 16: 15        37.12
 17: 1         85.05
 17: 2         73.05
 17: 3         66.03
 17: 4         61.05
 17: 5         57.19
 17: 6         54.03
 17: 7         51.36
 17: 8         49.05
 17: 9         47.01
 17: 10        45.19
 17: 11        43.54
 17: 12        42.03
 17: 13        40.64
 17: 14        39.36
 17: 15        38.17
 17: 16        37.05
 18: 1         86.04
 18: 5         58.18
 18: 7         52.35
 18: 11        44.53
 18: 13        41.63
 18: 17        36.99
 19: 1         86.98
 19: 2         74.98
 19: 3         67.96
 19: 4         62.98
 19: 5         59.11
 19: 6         55.96
 19: 7         53.29
 19: 8         50.98
 19: 9         48.94
 19: 10        47.11
 19: 11        45.46
 19: 12        43.96
 19: 13        42.57
 19: 14        41.29
 19: 15        40.09
 19: 16        38.98
 19: 17        37.93
 19: 18        36.94
 20: 1         87.86
 20: 3         68.84
 20: 7         54.17
 20: 9         49.82
 20: 11        46.35
 20: 13        43.46
 20: 17        38.81
 20: 19        36.89
 21: 1         88.71
 21: 2         76.71
 21: 4         64.71
 21: 5         60.84
 21: 8         52.71
 21: 10        48.84
 21: 11        47.19
 21: 13        44.3
 21: 16        40.71
 21: 17        39.66
 21: 19        37.73
 21: 20        36.84
 22: 1         89.51
 22: 3         70.49
 22: 5         61.65
 22: 7         55.82
 22: 9         51.47
 22: 13        45.11
 22: 15        42.63
 22: 17        40.46
 22: 19        38.54
 22: 21        36.81
 23: 1         90.28
 23: 2         78.28
 23: 3         71.26
 23: 4         66.28
 23: 5         62.42
 23: 6         59.26
 23: 7         56.59
 23: 8         54.28
 23: 9         52.24
 23: 10        50.42
 23: 11        48.77
 23: 12        47.26
 23: 13        45.88
 23: 14        44.59
 23: 15        43.4
 23: 16        42.28
 23: 17        41.23
 23: 18        40.24
 23: 19        39.31
 23: 20        38.42
 23: 21        37.57
 23: 22        36.77

 28: 1         93.69
 28: 3         74.67
 28: 5         65.83
 28: 9         55.65
 28: 11        52.18
 28: 13        49.28
 28: 15        46.81
 28: 17        44.64
 28: 19        42.71
 28: 23        39.41
 28: 25        37.96
 28: 27        36.63
 29: 1         94.3
 29: 2         82.3
 29: 3         75.28
 29: 4         70.3
 29: 5         66.43
 29: 6         63.28
 29: 7         60.61
 29: 8         58.3
 29: 9         56.26
 29: 10        54.43
 29: 11        52.78
 29: 12        51.28
 29: 13        49.89
 29: 14        48.61
 29: 15        47.41
 29: 16        46.3
 29: 17        45.25
 29: 18        44.26
 29: 19        43.32
 29: 20        42.43
 29: 21        41.59
 29: 22        40.78
 29: 23        40.01
 29: 24        39.28
 29: 25        38.57
 29: 26        37.89
 29: 27        37.24
 29: 28        36.61
 30: 1         94.88
 30: 7         61.19
 30: 11        53.37
 30: 13        50.48
 30: 17        45.83
 30: 19        43.91
 30: 23        40.6
 30: 29        36.59
 31: 1         95.45
 31: 2         83.45
 31: 3         76.43
 31: 4         71.45
 31: 5         67.59
 31: 6         64.43
 31: 7         61.76
 31: 8         59.45
 31: 9         57.41
 31: 10        55.59
 31: 11        53.94
 31: 12        52.43
 31: 13        51.05
 31: 14        49.76
 31: 15        48.57
 31: 16        47.45
 31: 17        46.4
 31: 18        45.41
 31: 19        44.48
 31: 20        43.59
 31: 21    42.74

 33: 1         96.53
 33: 2         84.53
 33: 4         72.53
 33: 5         68.67
 33: 7         62.84
 33: 8         60.53
 33: 10        56.67
 33: 13        52.13
 33: 14        50.84
 33: 16        48.53
 33: 17        47.48
 33: 19        45.56
 33: 20        44.67
 33: 23        42.25
 33: 25        40.81
 33: 26        40.13
 33: 28        38.84
 33: 29        38.24
 33: 31        37.08
 33: 32        36.53
 34: 1         97.05
 34: 3         78.03
 34: 5         69.19
 34: 7         63.36
 34: 9         59.01
 34: 11        55.54
 34: 13        52.64
 34: 15        50.17
 34: 19        46.07
 34: 21        44.34
 34: 23        42.77
 34: 25        41.32
 34: 27        39.99
 34: 29        38.75
 34: 31        37.6
 34: 33        36.52
 35: 1         97.55
 35: 2         85.55
 35: 3         78.53
 35: 4         73.55
 35: 6         66.53
 35: 8         61.55
 35: 9         59.51
 35: 11        56.04
 35: 12        54.53
 35: 13        53.15
 35: 16        49.55
 35: 17        48.5
 35: 18        47.51
 35: 19        46.58
 35: 22        44.04
 35: 23        43.27
 35: 24        42.53
 35: 26        41.15
 35: 27        40.49
 35: 29        39.26
 35: 31        38.1
 35: 32        37.55
 35: 33        37.02
 35: 34        36.5
 36: 1         98.04
 36: 5         70.18
 36: 7         64.35
 36: 11        56.53
 36: 13        53.63
 36: 17        48.99
 36: 19        47.06
 36: 23        43.76
 36: 25        42.31
 36: 29        39.74
 36: 31        38.59
 36: 35        36.49
 37: 1         98.51
 37: 2         86.51
 37: 3         79.49
 37: 4         74.51
 37: 5         70.65
 37: 6         67.49
 37: 7         64.83
 37: 8         62.51
 37: 9         60.47
 37: 10        58.65
 37: 11    57

39: 1 99.42

 39: 2         87.42
 39: 4         75.42
 39: 5         71.56
 39: 7         65.74
 39: 8         63.42
 39: 10        59.56
 39: 11        57.91
 39: 14        53.74
 39: 16        51.42
 39: 17        50.38
 39: 19        48.45
 39: 20        47.56
 39: 22        45.91
 39: 23        45.14
 39: 25        43.7
 39: 28        41.74
 39: 29        41.13
 39: 31        39.97
 39: 32        39.42
 39: 34        38.38
 39: 35        37.87
 39: 37        36.91
 39: 38        36.45
 40: 1         99.86
 40: 3         80.84
 40: 7         66.17
 40: 9         61.82
 40: 11        58.35
 40: 13        55.46
 40: 17        50.81
 40: 19        48.89
 40: 21        47.16
 40: 23        45.58
 40: 27        42.8
 40: 29        41.57
 40: 31        40.41
 40: 33        39.33
 40: 37        37.35
 40: 39        36.44
 41: 1         100.29
 41: 2         88.29
 41: 3         81.27
 41: 4         76.29
 41: 5         72.43
 41: 6         69.27
 41: 7         66.6
 41: 8         64.29
 41: 9         62.25
 41: 10        60.43
 41: 11        58.78
 41: 12        57.27
 41: 13        55.89
 41: 14        54.6
 41: 15        53.41
 41: 16        52.29
 41: 17        51.24
 41: 18        50.25
 41: 19        49.32
 41: 20        48.43
 41: 21        47.58
 41: 22        46.78
 41: 23        46.01
 41: 24        45.27
 41: 25        44.56
 41: 26        43.89
 41: 27        43.23
 41: 28    42.6

 43: 1         101.12
 43: 2         89.12
 43: 3         82.1
 43: 4         77.12
 43: 5         73.25
 43: 6         70.1
 43: 7         67.43
 43: 8         65.12
 43: 9         63.08
 43: 10        61.25
 43: 11        59.6
 43: 12        58.1
 43: 13        56.71
 43: 14        55.43
 43: 15        54.23
 43: 16        53.12
 43: 17        52.07
 43: 18        51.08
 43: 19        50.14
 43: 20        49.25
 43: 21        48.41
 43: 22        47.6
 43: 23        46.83
 43: 24        46.1
 43: 25        45.39
 43: 26        44.71
 43: 27        44.06
 43: 28        43.43
 43: 29        42.82
 43: 30        42.23
 43: 31        41.66
 43: 32        41.12
 43: 33        40.58
 43: 34        40.07
 43: 35        39.56
 43: 36        39.08
 43: 37        38.6
 43: 38        38.14
 43: 39        37.69
 43: 40        37.25
 43: 41        36.82
 43: 42    36.41

 45: 1         101.9
 45: 2         89.9
 45: 4         77.9
 45: 7         68.21
 45: 8         65.9
 45: 11        60.39
 45: 13        57.5
 45: 14        56.21
 45: 16        53.9
 45: 17        52.85
 45: 19        50.93
 45: 22        48.39
 45: 23        47.62
 45: 26        45.5
 45: 28        44.21
 45: 29        43.61
 45: 31        42.45
 45: 32        41.9
 45: 34        40.85
 45: 37        39.39
 45: 38        38.93
 45: 41        37.61
 45: 43        36.79
 45: 44        36.39

47: 1 102.66

 47: 2         90.66
 47: 3         83.64
 47: 4         78.66
 47: 5         74.79
 47: 6         71.64
 47: 7         68.97
 47: 8         66.66
 47: 9         64.62
 47: 10        62.79
 47: 11        61.14
 47: 12        59.64
 47: 13        58.25
 47: 14        56.97
 47: 15        55.77
 47: 16        54.66
 47: 17        53.61
 47: 18        52.62
 47: 19        51.68
 47: 20        50.79
 47: 21        49.95
 47: 22        49.14
 47: 23        48.37
 47: 24        47.64
 47: 25        46.93
 47: 26        46.25
 47: 27        45.6
 47: 28        44.97
 47: 29        44.36
 47: 30        43.77
 47: 31        43.2
 47: 32        42.66
 47: 33        42.12
 47: 34        41.61
 47: 35        41.1
 47: 36        40.62
 47: 37        40.14
 47: 38        39.68
 47: 39        39.23
 47: 40        38.79
 47: 41        38.36
 47: 42        37.95
 47: 43        37.54
 47: 44        37.14
 47: 45        36.75
 47: 46    36.37

8: 3 52.98

 8: 5          44.14
 8: 7          38.31
 9: 1          74.04
 9: 2          62.04
 9: 4          50.04
 9: 5          46.18
 9: 7          40.35
 9: 8          38.04
 10: 1         75.86
 10: 3         56.84
 10: 7         42.17
 10: 9         37.82
 11: 1         77.51
 11: 2         65.51
 11: 3         58.49
 11: 4         53.51
 11: 5         49.65
 11: 6         46.49
 11: 7         43.82
 11: 8         41.51
 11: 9         39.47
 11: 10        37.65
 12: 1         79.02
 12: 5         51.16
 12: 7         45.33
 12: 11        37.51
 13: 1         80.41
 13: 2         68.41
 13: 3         61.39
 13: 4         56.41
 13: 5         52.54
 13: 6         49.39
 13: 7         46.72
 13: 8         44.41
 13: 9         42.37
 13: 10        40.54
 13: 11        38.89
 13: 12        37.39
 14: 1         81.69
 14: 3         62.67
 14: 5         53.83
 14: 9         43.65
 14: 11        40.18
 14: 13        37.28
 15: 1         82.88
 15: 2         70.88
 15: 4         58.88
 15: 7         49.19
 15: 8         46.88
 15: 11        41.37
 15: 13        38.48
 15: 14        37.19
 16: 1         84

24: 1 91.02

 24: 5         63.16
 24: 7         57.33
 24: 11        49.51
 24: 13        46.61
 24: 17        41.97
 24: 19        40.04
 24: 23        36.74
 25: 1         91.73
 25: 2         79.73
 25: 3         72.71
 25: 4         67.73
 25: 6         60.71
 25: 7         58.04
 25: 8         55.73
 25: 9         53.69
 25: 11        50.21
 25: 12        48.71
 25: 13        47.32
 25: 14        46.04
 25: 16        43.73
 25: 17        42.68
 25: 18        41.69
 25: 19        40.75
 25: 21        39.02
 25: 22        38.21
 25: 23        37.44
 25: 24        36.71
 26: 1         92.41
 26: 3         73.39
 26: 5         64.54
 26: 7         58.72
 26: 9         54.37
 26: 11        50.89
 26: 15        45.52
 26: 17        43.36
 26: 19        41.43
 26: 21        39.7
 26: 23        38.12
 26: 25        36.68
 27: 1         93.06
 27: 2         81.06
 27: 4         69.06
 27: 5         65.2
 27: 7         59.37
 27: 8         57.06
 27: 10        53.2
 27: 11        51.55
 27: 13        48.65
 27: 14        47.37
 27: 16        45.06
 27: 17        44.01
 27: 19        42.08
 27: 20        41.2
 27: 22        39.55
 27: 23        38.78
 27: 25        37.33
 27: 26        36.65

31: 22 41.94

 31: 23        41.17
 31: 24        40.43
 31: 25        39.72
 31: 26        39.05
 31: 27        38.39
 31: 28        37.76
 31: 29        37.15
 31: 30        36.57
 32: 1         96
 32: 3         76.98
 32: 5         68.14
 32: 7         62.31
 32: 9         57.96
 32: 11        54.49
 32: 13        51.59
 32: 15        49.12
 32: 17        46.95
 32: 19        45.02
 32: 21        43.29
 32: 23        41.72
 32: 25        40.27
 32: 27        38.94
 32: 29        37.7
 32: 31        36.55

37: 12 55.49

 37: 13        54.11
 37: 14        52.83
 37: 15        51.63
 37: 16        50.51
 37: 17        49.46
 37: 18        48.47
 37: 19        47.54
 37: 20        46.65
 37: 21        45.81
 37: 22        45
 37: 23        44.23
 37: 24        43.49
 37: 25        42.79
 37: 26        42.11
 37: 27        41.45
 37: 28        40.83
 37: 29        40.22
 37: 30        39.63
 37: 31        39.06
 37: 32        38.51
 37: 33        37.98
 37: 34        37.46
 37: 35        36.96
 37: 36        36.47
 38: 1         98.98
 38: 3         79.96
 38: 5         71.11
 38: 7         65.29
 38: 9         60.94
 38: 11        57.46
 38: 13        54.57
 38: 15        52.09
 38: 17        49.93
 38: 21        46.27
 38: 23        44.69
 38: 25        43.25
 38: 27        41.92
 38: 29        40.68
 38: 31        39.52
 38: 33        38.44
 38: 35        37.42
 38: 37        36.46

41: 29 41.99

 41: 30        41.41
 41: 31        40.84
 41: 32        40.29
 41: 33        39.76
 41: 34        39.24
 41: 35        38.74
 41: 36        38.25
 41: 37        37.78
 41: 38        37.32
 41: 39        36.87
 41: 40        36.43
 42: 1         100.71
 42: 5         72.84
 42: 11        59.19
 42: 13        56.3
 42: 17        51.66
 42: 19        49.73
 42: 23        46.43
 42: 25        44.98
 42: 29        42.41
 42: 31        41.26
 42: 37        38.19
 42: 41        36.42

 44: 1         101.51
 44: 3         82.49
 44: 5         73.65
 44: 7         67.82
 44: 9         63.47
 44: 13        57.11
 44: 15        54.63
 44: 17        52.46
 44: 19        50.54
 44: 21        48.81
 44: 23        47.23
 44: 25        45.79
 44: 27        44.45
 44: 29        43.22
 44: 31        42.06
 44: 35        39.96
 44: 37        39
 44: 39        38.09
 44: 41        37.22
 44: 43        36.4

46: 1 102.28

 46: 3         83.26
 46: 5         74.42
 46: 7         68.59
 46: 9         64.24
 46: 11        60.77
 46: 13        57.88
 46: 15        55.4
 46: 17        53.23
 46: 19        51.31
 46: 21        49.57
 46: 25        46.56
 46: 27        45.22
 46: 29        43.99
 46: 31        42.83
 46: 33        41.75
 46: 35        40.73
 46: 37        39.77
 46: 39        38.86
 46: 41        37.99
 46: 43        37.17
 46: 45        36.38

48: 1 103.02

 48: 5         75.16
 48: 7         69.33
 48: 11        61.51
 48: 13        58.61
 48: 17        53.97
 48: 19        52.04
 48: 23        48.74
 48: 25        47.29
 48: 29        44.72
 48: 31        43.57
 48: 35        41.47
 48: 37        40.51
 48: 41        38.73
 48: 43        37.9
 48: 47        36.36

Hieronder hernemen we de lijst, maar nu in volgorde van klimmende toonhoogte, gesorteerd in zes kolommen van elk een oktaaf. Da's uiteraard een stuk handiger wanneer we 'juiste' toonladders willen samenstellen.

1 : 1 36

 48 : 47       36.36
 47 : 46       36.37
 46 : 45       36.38
 45 : 44       36.39
 44 : 43       36.4
 43 : 42       36.41
 42 : 41       36.42
 41 : 40       36.43
 40 : 39       36.44
 39 : 38       36.45
 38 : 37       36.46
 37 : 36       36.47
 36 : 35       36.49
 35 : 34       36.5
 34 : 33       36.52
 33 : 32       36.53
 32 : 31       36.55
 31 : 30       36.57
 30 : 29       36.59
 29 : 28       36.61
 28 : 27       36.63
 27 : 26       36.65
 26 : 25       36.68
 25 : 24       36.71
 24 : 23       36.74
 47 : 45       36.75
 23 : 22       36.77
 45 : 43       36.79
 22 : 21       36.81
 43 : 41       36.82
 21 : 20       36.84
 41 : 39       36.87
 20 : 19       36.89
 39 : 37       36.91
 19 : 18       36.94
 37 : 35       36.96
 18 : 17       36.99
 35 : 33       37.02
 17 : 16       37.05
 33 : 31       37.08
 16 : 15       37.12
 47 : 44       37.14
 31 : 29       37.15
 46 : 43       37.17
 15 : 14       37.19
 44 : 41       37.22
 29 : 27       37.24
 43 : 40       37.25
 14 : 13       37.28
 41 : 38       37.32
 27 : 25       37.33
 40 : 37       37.35
 13 : 12       37.39
 38 : 35       37.42
 25 : 23       37.44
 37 : 34       37.46
 12 : 11       37.51
 47 : 43       37.54
 35 : 32       37.55
 23 : 21       37.57
 34 : 31       37.6
 45 : 41       37.61
 11 : 10       37.65
 43 : 39       37.69
 32 : 29       37.7
 21 : 19       37.73
 31 : 28       37.76
 41 : 37       37.78
 10 : 9        37.82
 39 : 35       37.87
 29 : 26       37.89
 48 : 43       37.9
 19 : 17       37.93
 47 : 42       37.95
 28 : 25       37.96
 37 : 33       37.98
 46 : 41       37.99
 9 : 8         38.04
 44 : 39       38.09
 35 : 31       38.1
 26 : 23       38.12
 43 : 38       38.14
 17 : 15       38.17
 42 : 37       38.19
 25 : 22       38.21
 33 : 29       38.24
 41 : 36       38.25
 8 : 7         38.31
 47 : 41       38.36
 39 : 34       38.38
 31 : 27       38.39
 23 : 20       38.42
 38 : 33       38.44
 15 : 13       38.48
 37 : 32       38.51
 22 : 19       38.54
 29 : 25       38.57
 36 : 31       38.59
 43 : 37       38.6
 7 : 6         38.67
 48 : 41       38.73
 41 : 35       38.74
 34 : 29       38.75
 27 : 23       38.78
 47 : 40       38.79
 20 : 17       38.81
 33 : 28       38.84
 46 : 39       38.86
 13 : 11       38.89
 45 : 38       38.93
 32 : 27       38.94
 19 : 16       38.98
 44 : 37       39
 25 : 21       39.02
 31 : 26       39.05
 37 : 31       39.06
 43 : 36       39.08
 6 : 5         39.16
 47 : 39       39.23
 41 : 34       39.24
 35 : 29       39.26
 29 : 24       39.28
 23 : 19       39.31
 40 : 33       39.33
 17 : 14       39.36
 45 : 37       39.39
 28 : 23       39.41
 39 : 32       39.42
 11 : 9        39.47
 38 : 31       39.52
 27 : 22       39.55
 43 : 35       39.56
 16 : 13       39.59
 37 : 30       39.63
 21 : 17       39.66
 47 : 38       39.68
 26 : 21       39.7
 31 : 25       39.72
 36 : 29       39.74
 41 : 33       39.76
 46 : 37       39.77
 5 : 4         39.86
 44 : 35       39.96
 39 : 31       39.97
 34 : 27       39.99
 29 : 23       40.01
 24 : 19       40.04
 43 : 34       40.07
 19 : 15       40.09
 33 : 26       40.13
 47 : 37       40.14
 14 : 11       40.18
 37 : 29       40.22
 23 : 18       40.24
 32 : 25       40.27
 41 : 32       40.29
 9 : 7         40.35
 40 : 31       40.41
 31 : 24       40.43
 22 : 17       40.46
 35 : 27       40.49
 48 : 37       40.51
 13 : 10       40.54
 43 : 33       40.58
 30 : 23       40.6
 47 : 36       40.62
 17 : 13       40.64
 38 : 29       40.68
 21 : 16       40.71
 46 : 35       40.73
 25 : 19       40.75
 29 : 22       40.78
 33 : 25       40.81
 37 : 28       40.83
 41 : 31       40.84
 45 : 34       40.85
 4 : 3         40.98
 47 : 35       41.1
 43 : 32       41.12
 39 : 29       41.13
 35 : 26       41.15
 31 : 23       41.17
 27 : 20       41.2
 23 : 17       41.23
 42 : 31       41.26
 19 : 14       41.29
 34 : 25       41.32
 15 : 11       41.37
 41 : 30       41.41
 26 : 19       41.43
 37 : 27       41.45
 48 : 35       41.47
 11 : 8        41.51
 40 : 29       41.57
 29 : 21       41.59
 47 : 34       41.61
 18 : 13       41.63
 43 : 31       41.66
 25 : 18       41.69
 32 : 23       41.72
 39 : 28       41.74
 46 : 33       41.75
 7 : 5         41.83
 45 : 32       41.9
 38 : 27       41.92
 31 : 22       41.94
 24 : 17       41.97
 41 : 29       41.99
 17 : 12       42.03
 44 : 31       42.06
 27 : 19       42.08
 37 : 26       42.11
 47 : 33       42.12
 10 : 7        42.17
 43 : 30       42.23
 33 : 23       42.25
 23 : 16       42.28
 36 : 25       42.31
 13 : 9        42.37
 42 : 29       42.41
 29 : 20       42.43
 45 : 31       42.45
 16 : 11       42.49
 35 : 24       42.53
 19 : 13       42.57
 41 : 28       42.6
 22 : 15       42.63
 47 : 32       42.66
 25 : 17       42.68
 28 : 19       42.71
 31 : 21       42.74
 34 : 23       42.77
 37 : 25       42.79
 40 : 27       42.8
 43 : 29       42.82
 46 : 31       42.83
 3 : 2         43.02
 47 : 31       43.2
 44 : 29       43.22
 41 : 27       43.23
 38 : 25       43.25
 35 : 23       43.27
 32 : 21       43.29
 29 : 19       43.32
 26 : 17       43.36
 23 : 15       43.4
 43 : 28       43.43
 20 : 13       43.46
 37 : 24       43.49
 17 : 11       43.54
 48 : 31       43.57
 31 : 20       43.59
 45 : 29       43.61
 14 : 9        43.65
 39 : 25       43.7
 25 : 16       43.73
 36 : 23       43.76
 47 : 30       43.77
 11 : 7        43.82
 41 : 26       43.89
 30 : 19       43.91
 19 : 12       43.96
 46 : 29       43.99
 27 : 17       44.01
 35 : 22       44.04
 43 : 27       44.06
 8 : 5         44.14
 45 : 28       44.21
 37 : 23       44.23
 29 : 18       44.26
 21 : 13       44.3
 34 : 21       44.34
 47 : 29       44.36
 13 : 8        44.41
 44 : 27       44.45
 31 : 19       44.48
 18 : 11       44.53
 41 : 25       44.56
 23 : 14       44.59
 28 : 17       44.64
 33 : 20       44.67
 38 : 23       44.69
 43 : 26       44.71
 48 : 29       44.72
 5 : 3         44.84 
 47 : 28       44.97
 42 : 25       44.98
 37 : 22       45
 32 : 19       45.02
 27 : 16       45.06
 22 : 13       45.11
 39 : 23       45.14
 17 : 10       45.19
 46 : 27       45.22
 29 : 17       45.25
 41 : 24       45.27
 12 : 7        45.33 
 43 : 25       45.39
 31 : 18       45.41
 19 : 11       45.46
 45 : 26       45.5
 26 : 15       45.52
 33 : 19       45.56
 40 : 23       45.58
 47 : 27       45.6
 7 : 4         45.69
 44 : 25       45.79
 37 : 21       45.81
 30 : 17       45.83
 23 : 13       45.88
 39 : 22       45.91
 16 : 9        45.96
 41 : 23       46.01
 25 : 14       46.04
 34 : 19       46.07
 43 : 24       46.1
 9 : 5         46.18
 47 : 26       46.25
 38 : 21       46.27
 29 : 16       46.3
 20 : 11       46.35
 31 : 17       46.4
 42 : 23       46.43
 11 : 6        46.49
 46 : 25       46.56
 35 : 19       46.58
 24 : 13       46.61
 37 : 20       46.65
 13 : 7        46.72
 41 : 22       46.78
 28 : 15       46.81
 43 : 23       46.83
 15 : 8        46.88
 47 : 25       46.93
 32 : 17       46.95
 17 : 9        47.01
 36 : 19       47.06
 19 : 10       47.11
 40 : 21       47.16
 21 : 11       47.19
 44 : 23       47.23
 23 : 12       47.26
 48 : 25       47.29
 25 : 13       47.32
 27 : 14       47.37
 29 : 15       47.41
 31 : 16       47.45
 33 : 17       47.48
 35 : 18       47.51
 37 : 19       47.54
 39 : 20       47.56
 41 : 21       47.58
 43 : 22       47.6
 45 : 23       47.62
 47 : 24       47.64

2 : 1 48

 47 : 23       48.37
 45 : 22       48.39
 43 : 21       48.41
 41 : 20       48.43
 39 : 19       48.45
 37 : 18       48.47
 35 : 17       48.5
 33 : 16       48.53
 31 : 15       48.57
 29 : 14       48.61
 27 : 13       48.65
 25 : 12       48.71
 48 : 23       48.74
 23 : 11       48.77
 44 : 21       48.81
 21 : 10       48.84
 40 : 19       48.89
 19 : 9        48.94
 36 : 17       48.99
 17 : 8        49.05
 32 : 15       49.12
 47 : 22       49.14
 15 : 7        49.19
 43 : 20       49.25
 28 : 13       49.28
 41 : 19       49.32
 13 : 6        49.39
 37 : 17       49.46
 24 : 11       49.51
 35 : 16       49.55
 46 : 21       49.57
 11 : 5        49.65
 42 : 19       49.73
 31 : 14       49.76
 20 : 9        49.82
 29 : 13       49.89
 38 : 17       49.93
 47 : 21       49.95
 9 : 4         50.04
 43 : 19       50.14
 34 : 15       50.17
 25 : 11       50.21
 41 : 18       50.25
 16 : 7        50.31
 39 : 17       50.38
 23 : 10       50.42
 30 : 13       50.48
 37 : 16       50.51
 44 : 19       50.54
 7 : 3         50.67
 47 : 20       50.79
 40 : 17       50.81
 33 : 14       50.84
 26 : 11       50.89
 45 : 19       50.93
 19 : 8        50.98
 31 : 13       51.05
 43 : 18       51.08
 12 : 5        51.16
 41 : 17       51.24
 29 : 12       51.28
 46 : 19       51.31
 17 : 7        51.36
 39 : 16       51.42
 22 : 9        51.47
 27 : 11       51.55
 32 : 13       51.59
 37 : 15       51.63
 42 : 17       51.66
 47 : 19       51.68
 5 : 2         51.86
 48 : 19       52.04
 43 : 17       52.07
 38 : 15       52.09
 33 : 13       52.13
 28 : 11       52.18
 23 : 9        52.24
 41 : 16       52.29
 18 : 7        52.35
 31 : 12       52.43
 44 : 17       52.46
 13 : 5        52.54
 47 : 18       52.62
 34 : 13       52.64
 21 : 8        52.71
 29 : 11       52.78
 37 : 14       52.83
 45 : 17       52.85
 8 : 3         52.98
 43 : 16       53.12
 35 : 13       53.15
 27 : 10       53.2
 46 : 17       53.23
 19 : 7        53.29
 30 : 11       53.37
 41 : 15       53.41
 11 : 4        53.51
 47 : 17       53.61
 36 : 13       53.63
 25 : 9        53.69
 39 : 14       53.74
 14 : 5        53.83
 45 : 16       53.9
 31 : 11       53.94
 48 : 17       53.97
 17 : 6        54.03
 37 : 13       54.11
 20 : 7        54.17
 43 : 15       54.23
 23 : 8        54.28
 26 : 9        54.37
 29 : 10       54.43
 32 : 11       54.49
 35 : 12       54.53
 38 : 13       54.57
 41 : 14       54.6
 44 : 15       54.63
 47 : 16       54.66
 3 : 1         55.02
 46 : 15       55.4
 43 : 14       55.43
 40 : 13       55.46
 37 : 12       55.49
 34 : 11       55.54
 31 : 10       55.59
 28 : 9        55.65
 25 : 8        55.73
 47 : 15       55.77
 22 : 7        55.82
 41 : 13       55.89
 19 : 6        55.96
 35 : 11       56.04
 16 : 5        56.14
 45 : 14       56.21
 29 : 9        56.26
 42 : 13       56.3
 13 : 4        56.41
 36 : 11       56.53
 23 : 7        56.59
 33 : 10       56.67
 43 : 13       56.71
 10 : 3        56.84
 47 : 14       56.97
 37 : 11       57
 27 : 8        57.06
 44 : 13       57.11
 17 : 5        57.19
 41 : 12       57.27
 24 : 7        57.33
 31 : 9        57.41
 38 : 11       57.46
 45 : 13       57.5
 7 : 2         57.69
 46 : 13       57.88
 39 : 11       57.91
 32 : 9        57.96
 25 : 7        58.04
 43 : 12       58.1
 18 : 5        58.18
 47 : 13       58.25
 29 : 8        58.3
 40 : 11       58.35
 11 : 3        58.49
 48 : 13       58.61
 37 : 10       58.65
 26 : 7        58.72
 41 : 11       58.78
 15 : 4        58.88
 34 : 9        59.01
 19 : 5        59.11
 42 : 11       59.19
 23 : 6        59.26
 27 : 7        59.37
 31 : 8        59.45
 35 : 9        59.51
 39 : 10       59.56
 43 : 11       59.6
 47 : 12       59.64

4 : 1 60

 45 : 11       60.39
 41 : 10       60.43
 37 : 9        60.47
 33 : 8        60.53
 29 : 7        60.61
 25 : 6        60.71
 46 : 11       60.77
 21 : 5        60.84
 38 : 9        60.94
 17 : 4        61.05
 47 : 11       61.14
 30 : 7        61.19
 43 : 10       61.25
 13 : 3        61.39
 48 : 11       61.51
 35 : 8        61.55
 22 : 5        61.65
 31 : 7        61.76
 40 : 9        61.82
 9 : 2         62.04
 41 : 9        62.25
 32 : 7        62.31
 23 : 5        62.42
 37 : 8        62.51
 14 : 3        62.67
 47 : 10       62.79
 33 : 7        62.84
 19 : 4        62.98
 43 : 9        63.08
 24 : 5        63.16
 29 : 6        63.28
 34 : 7        63.36
 39 : 8        63.42
 44 : 9        63.47
 5 : 1         63.86
 46 : 9        64.24
 41 : 8        64.29
 36 : 7        64.35
 31 : 6        64.43
 26 : 5        64.54
 47 : 9        64.62
 21 : 4        64.71
 37 : 7        64.83
 16 : 3        64.98
 43 : 8        65.12
 27 : 5        65.2
 38 : 7        65.29
 11 : 2        65.51
 39 : 7        65.74
 28 : 5        65.83
 45 : 8        65.9
 17 : 3        66.03
 40 : 7        66.17
 23 : 4        66.28
 29 : 5        66.43
 35 : 6        66.53
 41 : 7        66.6
 47 : 8        66.66
 6 : 1         67.02
 43 : 7        67.43
 37 : 6        67.49
 31 : 5        67.59
 25 : 4        67.73
 44 : 7        67.82
 19 : 3        67.96
 32 : 5        68.14
 45 : 7        68.21
 13 : 2        68.41
 46 : 7        68.59
 33 : 5        68.67
 20 : 3        68.84
 47 : 7        68.97
 27 : 4        69.06
 34 : 5        69.19
 41 : 6        69.27
 48 : 7        69.33
 7 : 1         69.69
 43 : 6        70.1
 36 : 5        70.18
 29 : 4        70.3
 22 : 3        70.49
 37 : 5        70.65
 15 : 2        70.88
 38 : 5        71.11
 23 : 3        71.26
 31 : 4        71.45
 39 : 5        71.56
 47 : 6        71.64

8 : 1 72

 41 : 5        72.43
 33 : 4        72.53
 25 : 3        72.71
 42 : 5        72.84
 17 : 2        73.05
 43 : 5        73.25
 26 : 3        73.39
 35 : 4        73.55
 44 : 5        73.65
 9 : 1         74.04
 46 : 5        74.42
 37 : 4        74.51
 28 : 3        74.67
 47 : 5        74.79
 19 : 2        74.98
 48 : 5        75.16
 29 : 3        75.28
 39 : 4        75.42
 10 : 1        75.86
 41 : 4        76.29
 31 : 3        76.43
 21 : 2        76.71
 32 : 3        76.98
 43 : 4        77.12
 11 : 1        77.51
 45 : 4        77.9
 34 : 3        78.03
 23 : 2        78.28
 35 : 3        78.53
 47 : 4        78.66
 12 : 1        79.02
 37 : 3        79.49
 25 : 2        79.73
 38 : 3        79.96
 13 : 1        80.41
 40 : 3        80.84
 27 : 2        81.06
 41 : 3        81.27
 14 : 1        81.69
 43 : 3        82.1
 29 : 2        82.3
 44 : 3        82.49
 15 : 1        82.88
 46 : 3        83.26
 31 : 2        83.45
 47 : 3        83.64

16 : 1 84

 33 : 2        84.53
 17 : 1        85.05
 35 : 2        85.55
 18 : 1        86.04
 37 : 2        86.51
 19 : 1        86.98
 39 : 2        87.42
 20 : 1        87.86
 41 : 2        88.29
 21 : 1        88.71
 43 : 2        89.12
 22 : 1        89.51
 45 : 2        89.9
 23 : 1        90.28
 47 : 2        90.66
 24 : 1        91.02
 25 : 1        91.73
 26 : 1        92.41
 27 : 1        93.06
 28 : 1        93.69
 29 : 1        94.3
 30 : 1        94.88
 31 : 1        95.45

32 : 1 96

 33 : 1        96.53
 34 : 1        97.05
 35 : 1        97.55
 36 : 1        98.04
 37 : 1        98.51
 38 : 1        98.98
 39 : 1        99.42
 40 : 1        99.86
 41 : 1        100.29
 42 : 1        100.71
 43 : 1        101.12
 44 : 1        101.51
 45 : 1        101.9
 46 : 1        102.28
 47 : 1        102.66
 48 : 1        103.02

Bij wijze van voorbeeld, hierbij een van de vele mogelijke selekties, gegrepen uit bovenstaande tabellen, voor een juiste-boventoons kwarttoons stemming, met 24 noten per oktaaf:

1:1	35:34	18:17	12:11	9:8	15:13	19:16	11:9	29:23	13:10	4:3	11:8	17:12	16:11	3:2	17:11	27:17	18:11	32:19	19:11	16:9	11:6	17:9	35:18
36.00	36.50	36.99	37.51	38.04	38.48	38.98	39.47	40.01	40.54	40.98	41.51	42.03	42.49	43.02	43.54	44.01	44.53	45.02	45.46	45.96	46.49	47.01	47.51

Deze selektie benadert erg dicht de gelijkzwevende kwarttoonsstemming die we eerder al berekenden. Ze heeft iets onestetisch, omdat ze gebruik maakt van een erg groot aantal kwalitatief verschillende intervallen.

Heel wat van de muziek geschreven voor de 19e eeuw, en zeker voor de 18e eeuw uit onze kultuur is geschreven om te worden gespeeld in een of andere niet-gelijkzwevende stemming.. Het eigen klankkarakter dat werd toegeschreven aan de verschillende toonaarden en modi, is geheel en al op rekening te schrijven van het gebruik van niet-gelijkzwevende stemmingen. We gaan daar hier niet verder op in omdat het deel uitmaakt van elke goede kursus muziekgeschiedenis.

Merken we terloops nog op dat de gelijkzwevende stemming helemaal geen westerse uitvinding is, maar door de Chinezen werd ontwikkeld en ingevoerd in 1596, ongeveer een eeuw vooraleer dat bij ons het geval was. De systematisering van de gelijkzwevende stemming wordt toegeschreven aan Chu Tsai-Yu in de Ming dynastie (1368-1643). [cfr. M.Honegger, 'Science de la musique...", Bordas, Paris, 1976]

Niet gelijkzwevende stemmingen hebben ook in de twintigste eeuw heel wat voorvechters gekend: Harry Partch (die er zijn eigen instrumenten voor ontwikkelde), La Monte Young, Lou Harisson, Yvor Darregg, James Tenney, vele van de Californische komponisten uit de tweede helft van de twintigste eeuw. The Just Intonation Network is een organisatie die poogt alle komponisten die zich keren tegen de diktatuur van de twaalfde machtwortel uit twee, te verenigen. Het zal niemand verbazen dat heel wat van deze komponisten zich toeleggen op elektronische muziek: daarbinnen immers stelt het probleem van instrumentarium en speeltechniek zich nauwelijks.

'Real World' stemmingen en temperamenten...

In de vorige paragraaf toonden en bespraken we de fundamenten van niet gelijkzwevende stemmingen. We noemden ze Platonisch. Bij zulke stemmingen wordt steeds uitgegaan van een uitsluitend op een ideele werkelijkheid (een geloof) gesteund rekensysteem waarbinnen geen rekening gehouden wordt met de wetten van de fysika. Platonische in algemene , of pythagoreische in specifieke zin toonsystemen kunnen alleen enige betekenis hebben in een volstrekt 1-dimensioneel model van de werkelijkheid.. Ze zijn alleen denkbaar voor snaren zonder dikte noch massa, voor luchtkolommen zonder diameter en lucht zonder molekulen...

Geen enkel in de werkelijkheid bestaand objekt kan trillen en een boventoonreeks produceren die zich als een reeks gehele getallen verhoudt tot de grondtoon. Om die reden heeft ook geen enkele van de op konservatoria onderwezen 'harmonieleer'-varianten ook maar de geringste aanspraak op een fundament in de werkelijkheid noch in de fysika noch in de wetenschap in het algemeen. Ze is hooguit een deel van de theologie.

De trilling van een snaar van vlees-en-bloed kan alleen met een vierde graads differentiaal vergelijking benaderend worden beschreven. Het waarom daarvan behandelen we in onze kursus akoestiek. Deze feitelijkheid heeft natuurlijk enorme konsekwenties voor wie zich op spektra wil beroepen om een toonsysteem op te bouwen of te funderen.

Wanneer we de werkelijke spektrale reeks voor een werkelijke snaar berekenen zonder onverantwoord vergaande simplifikaties, dan blijkt dat spektrum niet alleen een funktie te zijn van de snaardikte, maar al evenzeer van de frekwentie zelf waarop die snaar gestemd wordt. De konsekwentie daarvan is dat het spektrum van elke snaar van een piano, bij wijze van voorbeeld, verschillend is. Bovendien blijkt dat het spektrum van een en dezelfde snaar veranderd naarmate we die snaar op een andere toon stemmen.

We voerden de berekening van de boventonen in het spektrum bij wijze van voorbeeld uit voor een nietomwikkelde piano snaar gestemd op Do (36). Ook nu nog maakten we enkele vereenvoudigingen:

we beschouwen de snaar als vrij trillend: dit wil zeggen, niet aangedreven door een strijkstok, plektrum of hamer
we beschouwen het spektrum als kontinu (dus onder weglating van de omhullende in de tijd)
we beschouwen niet de kleine ontstemming op het moment van en onmiddellijk na de botsing met de hamer
we beschouwen niet het spektrum van de torsie-komponent die nochtans steeds aanwezig is en een heel lage grondfrekwentie heeft.
we beschouwen niet de terugkoppeling op de trilwijze veroorzaakt door de klankkast en externe resonatoren
we beschouwen de snaarspektra los van de absolute amplitude. Nochtans heeft de amplitude onmiskenbare invloed op de klankkleur.
we beschouwen de snaren als homogeen, wat nochtans voor de omwikkelde snaren in sommige instrumenten niet het geval is.
we laten de longitudinale trillingsmodus van de snaar volledig buiten beschouwing

Wiskundig sluitende modellen voor het geheel van bovenstaande parameters bestaan voorzover wij weten, tot op heden niet. Wel weten we dat op grond van de vele vrijheidsgraden en parameters, we te maken zouden krijgen met een ingewikkeld stelsel van hogere orde differentiaalvergelijkingen. Om die reden kunnen er dan ook geen synthesizers bestaan die een 'goed' pianogeluid (niet van 'echt' te onderscheiden, bedoelen we dan) voortbrengen. De betere synthesizers proberen zelfs niet te 'synthesizen' maar maken gebruik van een sample-bank en reproduceren dus in werkelijkheid het geluid van echte opgenomen pianoklanken.

Parameters voor de volgende berekening:
Basisfrekwentie f(o):= 65.4064 Hz = Fractional note: 36

Berekend voor een snaarfaktor B = 3.333333E-4 (geldig voor de korresponderende snaar van een buffetpiano of kleine vleugel).

Formule: f(n) = n .f(0). SQR( 1 + B.n^2) , voor n >=1, in gehele getallen

Voor een snaar met dikte 0 is B=0 en krijgen we de hiervoor behandelde 'platonische' boventoonreeks.

B = E.mu.(Pi.r)^2 / (4.p.T.(L^2)) waarin

E = Youngs modulus voor het snaarmateriaal
mu = massa per lengteeenheid voor het snaarmateriaal
Pi = 3.14...
r = straal van de snaar (halve diameter)
p = densiteit van het materiaal
T = snaarspanning
L = snaarlengte

Boventoon-nummer , reele toonhoogte, 'platonische' toonhoogte, vershil in cent, verschil in Hz

Partial nr.: 1              real partial note: 36       Platonic Harmonic: 36       Dif= 0  cents  Dif= .01 Hz
Partial nr.: 2              real partial note: 48.01    Platonic Harmonic: 48       Dif= 1  cents  Dif= .09 Hz
Partial nr.: 3              real partial note: 55.05    Platonic Harmonic: 55.02    Dif= 3  cents  Dif= .29 Hz
Partial nr.: 4              real partial note: 60.05    Platonic Harmonic: 60       Dif= 5  cents  Dif= .7 Hz
Partial nr.: 5              real partial note: 63.93    Platonic Harmonic: 63.86    Dif= 7  cents  Dif= 1.36 Hz
Partial nr.: 6              real partial note: 67.12    Platonic Harmonic: 67.02    Dif= 10  cents Dif= 2.35 Hz
Partial nr.: 7              real partial note: 69.83    Platonic Harmonic: 69.69    Dif= 14  cents Dif= 3.72 Hz
Partial nr.: 8              real partial note: 72.18    Platonic Harmonic: 72       Dif= 18  cents Dif= 5.55 Hz
Partial nr.: 9              real partial note: 74.27    Platonic Harmonic: 74.04    Dif= 23  cents Dif= 7.89 Hz
Partial nr.: 10             real partial note: 76.15    Platonic Harmonic: 75.86    Dif= 28  cents Dif= 10.81 Hz
Partial nr.: 11             real partial note: 77.86    Platonic Harmonic: 77.51    Dif= 34  cents Dif= 14.37 Hz
Partial nr.: 12             real partial note: 79.43    Platonic Harmonic: 79.02    Dif= 41  cents Dif= 18.62 Hz
Partial nr.: 13             real partial note: 80.88    Platonic Harmonic: 80.41    Dif= 47  cents Dif= 23.62 Hz
Partial nr.: 14             real partial note: 82.24    Platonic Harmonic: 81.69    Dif= 55  cents Dif= 29.44 Hz
Partial nr.: 15             real partial note: 83.51    Platonic Harmonic: 82.88    Dif= 63  cents Dif= 36.13 Hz
Partial nr.: 16             real partial note: 84.71    Platonic Harmonic: 84       Dif= 71  cents Dif= 43.74 Hz
Partial nr.: 17             real partial note: 85.85    Platonic Harmonic: 85.05    Dif= 80  cents Dif= 52.33 Hz
Partial nr.: 18             real partial note: 86.93    Platonic Harmonic: 86.04    Dif= 89  cents Dif= 61.95 Hz
Partial nr.: 19             real partial note: 87.96    Platonic Harmonic: 86.98    Dif= 98  cents Dif= 72.65 Hz
Partial nr.: 20             real partial note: 88.95    Platonic Harmonic: 87.86    Dif= 108  cents Dif= 84.48 Hz
Partial nr.: 21             real partial note: 89.9     Platonic Harmonic: 88.71    Dif= 119  cents Dif= 97.49 Hz
Partial nr.: 22             real partial note: 90.81    Platonic Harmonic: 89.51    Dif= 129  cents Dif= 111.74 Hz
Partial nr.: 23             real partial note: 91.69    Platonic Harmonic: 90.28    Dif= 141  cents Dif= 127.25 Hz
Partial nr.: 24             real partial note: 92.54    Platonic Harmonic: 91.02    Dif= 152  cents Dif= 144.08 Hz
Partial nr.: 25             real partial note: 93.36    Platonic Harmonic: 91.73    Dif= 164  cents Dif= 162.28 Hz
Partial nr.: 26             real partial note: 94.16    Platonic Harmonic: 92.41    Dif= 176  cents Dif= 181.87 Hz
Partial nr.: 27             real partial note: 94.94    Platonic Harmonic: 93.06    Dif= 188  cents Dif= 202.91 Hz
Partial nr.: 28             real partial note: 95.7     Platonic Harmonic: 93.69    Dif= 201  cents Dif= 225.43 Hz
Partial nr.: 29             real partial note: 96.43    Platonic Harmonic: 94.3     Dif= 214  cents Dif= 249.46 Hz
Partial nr.: 30             real partial note: 97.15    Platonic Harmonic: 94.88    Dif= 227  cents Dif= 275.05 Hz
Partial nr.: 31             real partial note: 97.86    Platonic Harmonic: 95.45    Dif= 241  cents Dif= 302.23 Hz
Partial nr.: 32             real partial note: 98.54    Platonic Harmonic: 96       Dif= 254  cents Dif= 331.03 Hz
Partial nr.: 33             real partial note: 99.21    Platonic Harmonic: 96.53    Dif= 268  cents Dif= 361.48 Hz
Partial nr.: 34             real partial note: 99.87    Platonic Harmonic: 97.05    Dif= 282  cents Dif= 393.62 Hz
Partial nr.: 35             real partial note: 100.52   Platonic Harmonic: 97.55    Dif= 296  cents Dif= 427.47 Hz
Partial nr.: 36             real partial note: 101.15   Platonic Harmonic: 98.04    Dif= 311  cents Dif= 463.07 Hz
Partial nr.: 37             real partial note: 101.77   Platonic Harmonic: 98.51    Dif= 325  cents Dif= 500.43 Hz
Partial nr.: 38             real partial note: 102.38   Platonic Harmonic: 98.98    Dif= 340  cents Dif= 539.59 Hz
Partial nr.: 39             real partial note: 102.97   Platonic Harmonic: 99.42    Dif= 355  cents Dif= 580.57 Hz
Partial nr.: 40             real partial note: 103.56   Platonic Harmonic: 99.86    Dif= 370  cents Dif= 623.4 Hz
Partial nr.: 41             real partial note: 104.14   Platonic Harmonic: 100.29   Dif= 385  cents Dif= 668.09 Hz
Partial nr.: 42             real partial note: 104.71   Platonic Harmonic: 100.71   Dif= 400  cents Dif= 714.67 Hz
Partial nr.: 43             real partial note: 105.27   Platonic Harmonic: 101.12   Dif= 416  cents Dif= 763.17 Hz
Partial nr.: 44             real partial note: 105.82   Platonic Harmonic: 101.51   Dif= 431  cents Dif= 813.59 Hz
Partial nr.: 45             real partial note: 106.37   Platonic Harmonic: 101.9    Dif= 446  cents Dif= 865.97 Hz
Partial nr.: 46             real partial note: 106.9    Platonic Harmonic: 102.28   Dif= 462  cents Dif= 920.31 Hz
Partial nr.: 47             real partial note: 107.43   Platonic Harmonic: 102.66   Dif= 478  cents Dif= 976.64 Hz
Partial nr.: 48             real partial note: 107.95   Platonic Harmonic: 103.02   Dif= 493  cents Dif= 1034.98 Hz
Partial nr.: 49             real partial note: 108.47   Platonic Harmonic: 103.38   Dif= 509  cents Dif= 1095.33 Hz
Partial nr.: 50             real partial note: 108.97   Platonic Harmonic: 103.73   Dif= 525  cents Dif= 1157.71 Hz
Partial nr.: 51             real partial note: 109.47   Platonic Harmonic: 104.07   Dif= 540  cents Dif= 1222.15 Hz
Partial nr.: 52             real partial note: 109.97   Platonic Harmonic: 104.41   Dif= 556  cents Dif= 1288.65 Hz
Partial nr.: 53             real partial note: 110.46   Platonic Harmonic: 104.74   Dif= 572  cents Dif= 1357.23 Hz
Partial nr.: 54             real partial note: 110.94   Platonic Harmonic: 105.06   Dif= 588  cents Dif= 1427.89 Hz
Partial nr.: 55             real partial note: 111.41   Platonic Harmonic: 105.38   Dif= 604  cents Dif= 1500.66 Hz
Partial nr.: 56             real partial note: 111.88   Platonic Harmonic: 105.69   Dif= 619  cents Dif= 1575.54 Hz
Partial nr.: 57             real partial note: 112.35   Platonic Harmonic: 105.99   Dif= 635  cents Dif= 1652.55 Hz
Partial nr.: 58             real partial note: 112.81   Platonic Harmonic: 106.3    Dif= 651  cents Dif= 1731.69 Hz
Partial nr.: 59             real partial note: 113.26   Platonic Harmonic: 106.59   Dif= 667  cents Dif= 1812.98 Hz
Partial nr.: 60             real partial note: 113.71   Platonic Harmonic: 106.88   Dif= 683  cents Dif= 1896.42 Hz
Partial nr.: 61             real partial note: 114.15   Platonic Harmonic: 107.17   Dif= 698  cents Dif= 1982.03 Hz
Partial nr.: 62             real partial note: 114.59   Platonic Harmonic: 107.45   Dif= 714  cents Dif= 2069.81 Hz
Partial nr.: 63             real partial note: 115.02   Platonic Harmonic: 107.73   Dif= 730  cents Dif= 2159.77 Hz
Partial nr.: 64             real partial note: 115.45   Platonic Harmonic: 108      Dif= 745  cents Dif= 2251.92 Hz
Partial nr.: 65             real partial note: 115.88   Platonic Harmonic: 108.27   Dif= 761  cents Dif= 2346.27 Hz
Partial nr.: 66             real partial note: 116.3    Platonic Harmonic: 108.53   Dif= 776  cents Dif= 2442.83 Hz
Partial nr.: 67             real partial note: 116.71   Platonic Harmonic: 108.79   Dif= 792  cents Dif= 2541.6 Hz
Partial nr.: 68             real partial note: 117.12   Platonic Harmonic: 109.05   Dif= 807  cents Dif= 2642.59 Hz
Partial nr.: 69             real partial note: 117.53   Platonic Harmonic: 109.3    Dif= 823  cents Dif= 2745.8 Hz
Partial nr.: 70             real partial note: 117.93   Platonic Harmonic: 109.55   Dif= 838  cents Dif= 2851.25 Hz
Partial nr.: 71             real partial note: 118.33   Platonic Harmonic: 109.8    Dif= 853  cents Dif= 2958.94 Hz
Partial nr.: 72             real partial note: 118.73   Platonic Harmonic: 110.04   Dif= 869  cents Dif= 3068.86 Hz
Partial nr.: 73             real partial note: 119.12   Platonic Harmonic: 110.28   Dif= 884  cents Dif= 3181.04 Hz
Partial nr.: 74             real partial note: 119.5    Platonic Harmonic: 110.51   Dif= 899  cents Dif= 3295.47 Hz
Partial nr.: 75             real partial note: 119.89   Platonic Harmonic: 110.75   Dif= 914  cents Dif= 3412.17 Hz
Partial nr.: 76             real partial note: 120.27   Platonic Harmonic: 110.98   Dif= 929  cents Dif= 3531.12 Hz

De spektraaltonen zijn allemaal een beetje tot een heel stuk groter dan het platonische model zou laten uitschijnen. Bij de veertiende boventoon, beloopt het verschil al meer dan een kwarttoon. De negentiende bovendien, zit al een halve toon 'fout'. Bij de 61-ste bovendien beloopt het verschil al een kwint... De waarneembaarheid van deze wel erg hoge boventonen is evenwel betwijfelbaar. Immers de amplitude van de spektraalkomponenten neemt af volgens een voor elke spektraaltoon eigen omhullende, globaal echter evenredig met hun rangorde. Praktisch gesproken kunnen we voor vrij klinkende snaren alle spektraalkomponenten met een rangnummer groter dan 20 buiten beschouwing laten, wegens beneden de gehoordrempel. (Memo: voor aangeslagen snaren vormen de amplitudes van de boventonen een reeks van de vorm 1, 1/2, 1/3, 1/3, 1/4.... 1/n. Voor getokkelde snaren heeft de reeks de vorm: 1, 1/2^2, 1/3^2, 1/4^2, 1/5^2... 1/n^2. cfr: 4040.html).

Een goede verstaander zal het intussen al doorhebben: Indien we een stemming zouden willen steunen op de werkelijke boventonen van werkelijke snaren dan zal dat onmogelijk blijken omdat elke snaar nu eenmaal een ander spektrum zal hebben. Zelfs een stemming berekend voor een instrument met 1 enkele snaar en fretten voor de verschillende toonhoogtes kan niet toonsysteem-konsistent gebouwd en berekend worden. Sterker nog, gesteld dat we het waanzinnige idee in ons hoofd zouden halen om verschillende instrumenten, snaarinstrumenten enerzijds en instrumenten gesteund op trillende luchtkolommen anderzijds, samen te laten spelen, dan worden we onherroepelijk gekonfronteerd met het akoestische feit dat voor trillende luchtkolommen evenzeer geldt wat we stelden in verband met de inharmoniciteit van snaren, maar dan... in omgekeerde richting: de spektraalkomponenten blijken hier systematisch een beetje te klein te zijn. Zelfs een gewoon unisono wordt onmogelijk...

Maar, we kunnen deze verschikkelijke ellende ook in ons voordeel laten uitdraaien: precies omdat de spektra van reeele instrumenten niet alleen inharmonisch zijn, maar bovendien volkomen inkongruent, zijn wij audioperceptorisch in staat de diverse geluidsbronnen in het bonte mengsel dat een orkest wordt genoemd, te onderscheiden. Het is precies in en dankzij de anarchie van de klinkende werkelijkheid, dat de individuele stem hoorbaar kan worden.

Een verdere konsekwentie van de wetenschappelijke akoestiek is dat alle 'juiste boventoons' stemmingen in hun grondvesten naar het rijk der fabeltjes worden verwezen. Gelijkzwevende stemmingen -het aantal verdelingen per oktaaf doet er hier verder niet toe- vormen een heel goed kompromis wanneer we snaren en windinstrumenten samen willen laten spelen.

Wanneer we evenwel grotendeels aan beide verzaken, en bijvoorbeeld orkesten samenstellen met hoofdzakelijk twee- en drie-dimensioneel trillende voorwerpen (gongs, potgongs, bellen, platen, staven...) dan komen we inzake toonsystemen en stemmingen alweer in een geheel andere wereld terecht. De javaanse en balinese gamelan-kultuur heeft inderdaad een toonsysteem tot ontwikkeling gebracht, dat voor een groot stuk kan worden verklaard op grond van het gebruikte instrumentarium. Vergeten we immers niet dat de spektra van trillende platen en membranen in verste verte geen kwinten en oktaven bevatten! Gamelan orkesten worden gestemd en geintoneerd op grond van de boventonen van hun grootste gongs. Elk gamelan orkest heeft dan ook een eigen intonatie en de instrumenten van de ene gamelan zijn niet zonder meer uitwisselbaar voor die van een ander.

Voor wie na het na het bovenstaande nog niet zou beginnen te dagen, hebben we ook een berekening gemaakt voor het spektrum van een lage omwikkelde snaar in een kleine vleugel of buffetpiano.

Basisfrekwentie:= 65.4064 Hz = Fractional note: 36 Berekend voor een snaarfaktor B= 5.694346E-3, overeenkomend met volgende realistische snaareigenschappen:

snaardiameter: 2.75 mm
kracht: 850 N
Lengte = 107 cm
Elasticiteitsmodulus: 2E11
densiteit: 7.3 kg/dm3

Partial nr.: 1              real partial note: 36.00    Plato-Harmonic: 36          Dif= 0  cent     Dif= 0 Hz
Partial nr.: 2              real partial note: 48.19    Plato-Harmonic: 48          Dif= 19  cent    Dif= 1.48 Hz
Partial nr.: 3              real partial note: 55.45    Plato-Harmonic: 55.02       Dif= 43  cent    Dif= 4.97 Hz
Partial nr.: 4              real partial note: 60.75    Plato-Harmonic: 60          Dif= 75  cent    Dif= 11.66 Hz
Partial nr.: 5              real partial note: 65.02    Plato-Harmonic: 63.86       Dif= 115  cent    Dif= 22.5 Hz
Partial nr.: 6              real partial note: 68.63    Plato-Harmonic: 67.02       Dif= 161  cent    Dif= 38.35 Hz
Partial nr.: 7              real partial note: 71.82    Plato-Harmonic: 69.69       Dif= 213  cent    Dif= 59.95 Hz
Partial nr.: 8              real partial note: 74.69    Plato-Harmonic: 72          Dif= 269  cent    Dif= 87.95 Hz
Partial nr.: 9              real partial note: 77.32    Plato-Harmonic: 74.04       Dif= 328  cent    Dif= 122.92 Hz
Partial nr.: 10             real partial note: 79.76    Plato-Harmonic: 75.86       Dif= 390  cent    Dif= 165.33 Hz
Partial nr.: 11             real partial note: 82.05    Plato-Harmonic: 77.51       Dif= 454  cent    Dif= 215.57 Hz
Partial nr.: 12             real partial note: 84.2     Plato-Harmonic: 79.02       Dif= 518  cent    Dif= 273.98 Hz
Partial nr.: 13             real partial note: 86.24    Plato-Harmonic: 80.41       Dif= 584  cent    Dif= 340.83 Hz
Partial nr.: 14             real partial note: 88.18    Plato-Harmonic: 81.69       Dif= 649  cent    Dif= 416.35 Hz
Partial nr.: 15             real partial note: 90.02    Plato-Harmonic: 82.88       Dif= 714  cent    Dif= 500.73 Hz
Partial nr.: 16             real partial note: 91.78    Plato-Harmonic: 84          Dif= 778  cent    Dif= 594.12 Hz
Partial nr.: 17             real partial note: 93.47    Plato-Harmonic: 85.05       Dif= 842  cent    Dif= 696.67 Hz
Partial nr.: 18             real partial note: 95.09    Plato-Harmonic: 86.04       Dif= 905  cent    Dif= 808.47 Hz
Partial nr.: 19             real partial note: 96.64    Plato-Harmonic: 86.98       Dif= 967  cent    Dif= 929.61 Hz
Partial nr.: 20             real partial note: 98.14    Plato-Harmonic: 87.86       Dif= 1028  cent    Dif= 1060.18 Hz
Partial nr.: 21             real partial note: 99.58    Plato-Harmonic: 88.71       Dif= 1087  cent    Dif= 1200.22 Hz
Partial nr.: 22             real partial note: 100.97   Plato-Harmonic: 89.51       Dif= 1146  cent    Dif= 1349.81 Hz
Partial nr.: 23             real partial note: 102.31   Plato-Harmonic: 90.28       Dif= 1203  cent    Dif= 1508.97 Hz
Partial nr.: 24             real partial note: 103.61   Plato-Harmonic: 91.02       Dif= 1259  cent    Dif= 1677.76 Hz
Partial nr.: 25             real partial note: 104.86   Plato-Harmonic: 91.73       Dif= 1313  cent    Dif= 1856.19 Hz
Partial nr.: 26             real partial note: 106.07   Plato-Harmonic: 92.41       Dif= 1367  cent    Dif= 2044.3 Hz
Partial nr.: 27             real partial note: 107.25   Plato-Harmonic: 93.06       Dif= 1419  cent    Dif= 2242.12 Hz
Partial nr.: 28             real partial note: 108.39   Plato-Harmonic: 93.69       Dif= 1470  cent    Dif= 2449.65 Hz
Partial nr.: 29             real partial note: 109.5    Plato-Harmonic: 94.3        Dif= 1520  cent    Dif= 2666.92 Hz
Partial nr.: 30             real partial note: 110.57   Plato-Harmonic: 94.88       Dif= 1569  cent    Dif= 2893.95 Hz
Partial nr.: 31             real partial note: 111.62   Plato-Harmonic: 95.45       Dif= 1617  cent    Dif= 3130.74 Hz
Partial nr.: 32             real partial note: 112.63   Plato-Harmonic: 96          Dif= 1663  cent    Dif= 3377.31 Hz
Partial nr.: 33             real partial note: 113.62   Plato-Harmonic: 96.53       Dif= 1709  cent    Dif= 3633.67 Hz
Partial nr.: 34             real partial note: 114.59   Plato-Harmonic: 97.05       Dif= 1754  cent    Dif= 3899.83 Hz
Partial nr.: 35             real partial note: 115.52   Plato-Harmonic: 97.55       Dif= 1797  cent    Dif= 4175.79 Hz
Partial nr.: 36             real partial note: 116.44   Plato-Harmonic: 98.04       Dif= 1840  cent    Dif= 4461.56 Hz
Partial nr.: 37             real partial note: 117.33   Plato-Harmonic: 98.51       Dif= 1882  cent    Dif= 4757.14 Hz
Partial nr.: 38             real partial note: 118.21   Plato-Harmonic: 98.98       Dif= 1923  cent    Dif= 5062.55 Hz
Partial nr.: 39             real partial note: 119.06   Plato-Harmonic: 99.42       Dif= 1963  cent    Dif= 5377.78 Hz
Partial nr.: 40             real partial note: 119.89   Plato-Harmonic: 99.86       Dif= 2003  cent    Dif= 5702.84 Hz
Partial nr.: 41             real partial note: 120.7    Plato-Harmonic: 100.29      Dif= 2041  cent    Dif= 6037.74 Hz

De resultaten mogen in dit geval zeker spektakulair worden genoemd. Zelfs de eerste boventoon, het oktaaf vertoont nu reeds twee zwevingen. Dit verschijnsel ligt trouwens aan de basis van het door alle goede pianostemmers toegepaste 'ecartement': de vergroting van de oktaven in de lage bassen en bij de extreme hoogten.

De wetenschappelijke eerlijkheid en ernst verplicht er ons, naar aanleiding van bovenstaande berekening, toch volgende opmerkingen te maken:

- we maakten abstraktie van het feit dat deze snaar omwikkeld is, waardoor zij eigenlijk niet als homogeen kan worden beschouwd. De densiteit (die we hier gelijk stelden aan die voor staal) zou dan ook beter bepaald worden als gemiddelde tussen koper en staal in de verhouding van de respektievelijke volumes. Ze zal in elk geval hoger komen te liggen. De inharmoniciteit zal hierdoor eerder nog wat toenemen.
- de omwikkeling met koper is lateraal over de stalen kern heen: hierdoor wordt de snaar elastischer en veranderd de elasticiteitsmodulus. Exakte waarden zijn ons evenwel niet bekend. Dit gegeven kan in mindering gebracht worden van de inharmoniciteit.
- de snaar is aan de uiteinden niet omwikkeld: de doorsnede is dus niet konstant over de lengte. Dit brachten we niet in rekening, maar zeker is wel dat dit de inharmoniciteit nog vergroot..

'Wohltemperiert' - 'well tempered'

Parentesis

Tot de gelijkzwevende stemming in de west europese muziek algemeen ingang vond, kende onze muziekkultuur een veelheid aan verschillende stemmingen en toonsystemen. In de tijd van J.S.Bach vond de term 'wohltemperiert' ingang. De term verwijst niet -voorzover men heeft kunnen nagaan- naar een welgedefinieerd stemmingssysteem, maar wel naar een principe dat toen ingang vond en dat erop neerkomt dat men de problemen van elke juiste boventoonsstemming vanzodra men gaat moduleren, poogt te ondervangen door de fout van de komma, te verspreiden over een aantal intervallen.

Een gangbaar systeem (maar er zijn er teveel om op te noemen of hier te behandelen) om dit te doen gaat alsvolgt:

[berekening overgenomen uit: Philippe Guillaume, Music and Acoustics, ISTE, London 2006]

Uitgaand van de centrale Do, gaan we door een cyclus van 4 identieke kwinten: do-sol-re-la-mi die we elk zo stemmen dat ze een beetje te laag staan en wel zodanig dat het aantal zwevingen van do-sol gelijk is aan dat van de terts do-mi, die dan een zweving te hoog gestemd moet worden.

Noemen we x de gebruikte verhouding voor de kwint, en f de frekwentie voor onze do dan kunnen we stellen:

zweving van de terts do-mi: b1= |(5-4x^2/4)| * f = ((x^4) -5)* f

zweving van de kwint do-sol: b2 = |(3-(2*x)| * f = (3-(2*x)) *f

als nu b1 = b2 volgens onze konditie (zelfde zweving voor terts en kwint) dan moeten we hebben:

(x^4) + (2*x) - 8 = 0

een tweede-graads vergelijking met als oplossing x = 1.496

De kwint si- fa# wordt nu volgens deze verhouding gestemd en alle overige kwinten juist in de 3:2 verhouding. De oktaven worden zwevingsvrij gestemd, wat mogelijk is omdat:

(x^5) * (3/2)^7 = 128.006, dus kwazi 128.

Het resultaat is een stemming waarin alle grote tertsen iets verschillend zijn en telkens in geringe mate afwijken van de juiste boventoonsterts. Naarmate we van do-groot gaan wegmoduleren of transponeren, veranderen onze tertsen dus weg van het boventoonsideaal.

Het muzikaal estetisch gevolg is dat elke modulatie in een andere toonaard een eigen inkleuring krijgt, terwijl toch geen enkele toonaard onbeluisterbaar dissonant zal klinken. Dat was wellicht wat Bach wilde aantonen en bereiken in zijn 'Das Wohltemperirte Clavier'

Filedate: /2007-03-26 / rev.28.03.2011

DO - RE	RE -MI	MI - FA	FA - SOL	SOL - LA	LA -SI	SI -DO
(9:8)/(1:1)= 9:8	(5:4)/(9:8) = 10: 9	(4:3) / (5:4) = 16:15	(3:2) / (4:3) = 9:8	(5:3)/ (3:2) =10:9	(15:8)/(5:3) = 9:8	(1:2)/(15:8) = 16:15