Prof.dr.Godfried-Willem RAES
Kursus Akoestiek
Hogeschool Gent : School of Arts
| <Terug naar inhoudstafel kursus> | Naar index boekdeel akoestiek |
4400
Klank en Ruimte
1.- Open ruimtes
In onze inleiding hadden we het -enigszins terloops- over de open ruimte, gekarakteriseerd door een 'nul-akoestiek'. Typisch daarvoor is dat niets van de van een geluidsbron uitgaande trilling wordt weerkaatst door enig obstakel. Dit is wat we zouden kunnen noemen, de akoestische omgeving van de valschermspringer of ballonvaarder (tenminste wanneer we de reflekties door de ballon buiten beschouwing laten). Deze situatie is ideaal voor het uitvoeren van akoestische proefnemingen, maar wordt geplaagd door de onhebbelijkheden van de open ruimte: wind, regen, natuurlijk omgevingslawaai en geluidspolutie van menselijke oorsprong, veranderlijke temperatuur enz... kunnen allemaal roet in het meettechnische eten strooien. Om aan die problemen te ontkomen is men algauw zgn. akoestisch dode ruimtes gaan bouwen, waarbij door de vorm van de ruimte enerzijds en door het aanbrengen van allerlei dempingsmaterialen toch zoiets als een nul-akoestiek kan worden benaderd. In Gent beschikt voorzover wij weten alleen het technikum van de universiteit (Sint-Pietersnieuwstraat) over een (kleine) akoestisch dode ruimte. Anechoische ruimtes -de technische term voor de dode kamers- zijn onontbeerlijk voor metingen aan muziekinstrumenten, luidsprekers, mikrofoons, machines en werktuigen, motoren. Dus, zowel voor gevallen waarin het geproduceerd geluid wenselijk is als in die waarin het integendeel zoveel mogelijk dient te worden vermeden. Anechoische ruimten zijn steeds voorzien van zeer goede betrouwbare en gekallibreerde meetmikrofoons. Meetgegevens die op die wijze verkregen worden zijn bvb. frekwentiekarakteristiek, afstraalkarakteristiek, spektrum, geluidsdruk, omhullende. Voor muziekopnames zijn dergelijke ruimtes volstrekt ongeschikt, niet in de laatste plaats omdat er niet in te musiceren valt vanwege de ondermijning van de audio-feedback die essentieel is bij het bespelen van een muziekinstrument.
Zoals we zagen in de inleiding, moet een geluidsbron in een vrije ruimte beschouwd worden als een omnidirektionele straler. De minimale afstand waarop geldige metingen kunnen worden uitgevoerd, moet evenwel steeds groter zijn dan de volledige golflengte van de laagste voortgebrachte frekwentie en bovendien veel groter dan de grootste afmeting van de geluidsbron. Onder die kondities kunnen we stellen dat de geluidsenergie zich over de ruimte verspreid als een uitdeinende bol. Op 1 meter afstand van een kleine bron, is de oppervlakte van die bol ca. 12,5 vierkante meter. Ons oor (oorschelp reflektor inbegrepen) heeft een oppervlakte van hooguit 12 vierkante centimeter. Daarom is het deel van de akoestische uitgestraalde energie dat door ons oor wordt opgevangen slechts 125.000 / 12 = 10.416, of ongeveer een tienduizendste van de totale afgestraalde energie. Wanneer je nu tweemaal verder van de bron afgaat, op 2 meter dus in ons voorbeeld, dan wordt deze verhouding 502.655 / 12 = 41.888, of nog slechts een kwart van die energie. (memo: oppervlakte van een bol = Pi * d^2 of 4 * Pi * r^2). Dit illustreert ten overvloede de omgekeerd kwadratische afhankelijkheid van de geluidsdruk van de afstand tot de bron.
We halen deze informatie nog eens opnieuw op, omdat ze ons een goed idee geeft van de enorme hoeveelheid geluidsenergie die voor de menselijke perceptie verloren gaat in de ruimte, wanneer deze volkomen vrij van obstakels is. Een bolvormige ruimtestraler wordt gekenmerkt door een direktiviteits- of richtingsfaktor gelijk aan 1. (Q=1).
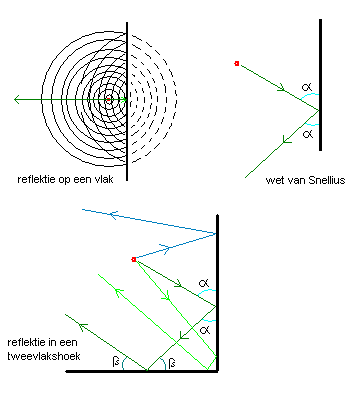
Wanneer we een 'oneindig' en perfekt reflekterend vlak aanbrengen vlak bij de geluidsbron, dan wordt onze bolvormige straler een halve bol. Het onmiddellijke gevolg is duidelijk: de geluidsenergie wordt nu over de helft van de ruimte afgestraald en dus moet de energie per oppervlakte eenheid nu het dubbele bedragen. (+6dB toename van de geluidsdruk). Wanneer we een grote reflekterende wand achter een muzikant plaatsen, dan klinkt deze in de praktijk even luid als twee muzikanten zonder wand erachter. Een hemisferische straler wordt gekenmerkt door een direktiviteitsfaktor Q = 2.

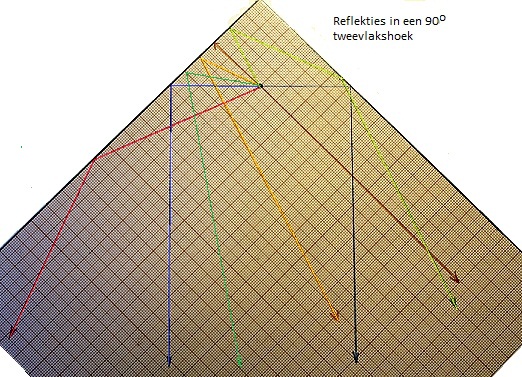
Dezelfde redenering volgend, kunnen we nu de geluidsbron plaatsen in een tweevlakshoek, gevormd door twee 'oneindige' reflekterende vlakken, loodrecht op elkaar geplaatst. De ruimte wordt nu een kwartruimte, de direktiviteitsfaktor wordt Q= 4 en de afgestraalde geluidsenergie neemt toe met een faktor 4. (12dB) (cfr. onderste tekening).
Aangezien we in de ruimte maksimaal 3 dimensies hebben, kunnen we tenslotte nog 1 stap verder gaan door onze geluidsbron op te stellen in de hoek van een drievlakshoek. De ruimte wordt nu een achtsteruimte, Q=8, en de geluidsenergie per oppervlakteeenheid neemt toe met een faktor 8 (18dB).
Stel nu dat we onze vlakken niet onder rechte hoeken plaatsen, maar die hoek verkleiner, dan krijgen we een toeter of megafoon, en wordt de geluidsdruk alsmaar groter naarmate de hoek kleiner wordt. Voor ruimtehoeken van 60 graden (een tetraederhoek) krijgen we een maximale geluidsdruk waarbij net nog geen staande golven kunnen optreden. (Q= 12, of een maximale geluidsdruktoename per oppervlakteeenheid van 22dB).

Maken we de hoek nog kleiner, dan neemt de geluidsdruk weliswaar verder toe, maar dan is die toename mede afhankelijk van de golflengte van het geluid. Dit principe ligt ten andere aan de basis van de toeters gevormd op zowat alle koperblaasinstrumenten, de megafoons, van grammofoons etc... De wetmatigheden daarvan worden verder behandeld wanneer we het over deze instrumenten en geluidsweergevers hebben.
Opgemerkt moet worden dat de hier vermelde winst aan geluidsdruk overeenkomt met een teoretisch maximum, dat in de praktijk nooit kan worden gehaald. Enerzijds niet, omdat geen vlak ooit perfekt reflekterend is, en verder nog omdat een deel van het geluid steeds als warmte verloren zal gaan. De botsing van luchtmolekulen is immers nooit perfekt elastisch. Uiteindelijk lost alle geluid trouwens op in warmte... Dus, zelfs al zouden we over een perfekt doosje beschikken, dan nog zouden we er nooit een geluid in kunnen opsluiten en bewaren, zoals enkele Franse geleerden nog tot op het eind van de 18e eeuw dachten.
Nota: [ lineaire stralers] 4405.html
2. Gesloten ruimtes
In meer 'normale' ruimtelijke omstandigheden evenwel, worden geluidsgolven door allerlei obstakels die niet steeds 'vlakken' zijn alsmaar weer weerkaatst waardoor een geluid nog een tijd hoorbaar blijft nadat de bron stom werd. Dit verschijnsel wordt algemeen met de term 'galm' of 'nagalm' omschreven. (reverb). Een obstakel funktioneert in de akoestiek als een sekundaire geluidsbron, wanneer de reflektie eigenschappen ervan dit toelaten. Een volledig absorberend obstakel (een open raam bvb.) is equivalent aan de open ruimte en reflekteert helemaal niets. Een geklede persoon geldt akoestisch als het equivalent van een halve vierkante meter open raam, vandaar het verschil in akoestische eigenschappen van een lege zaal versus een volledig bezette zaal.
De kurve waarbij horizontaal het tijdsverloop en vertikaal de geluidsdruk in decibell wordt voorgesteld, is karakteristiek voor elke ruimte en noemen we de galmkurve van de ruimte.
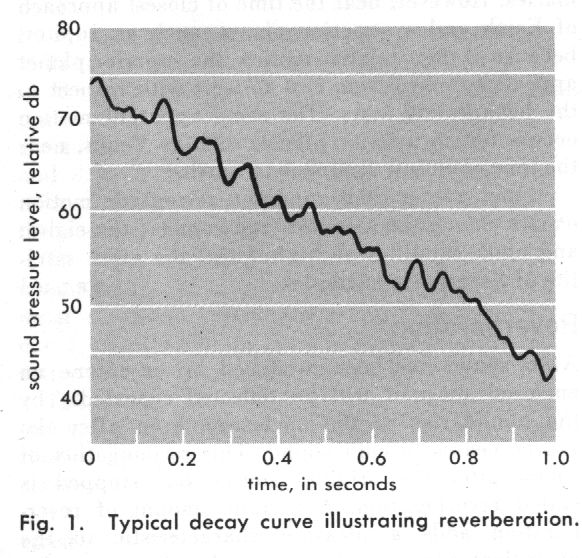
Het globaal afnemend verloop van deze kurve verloopt nagenoeg nooit regelmatig, maar vertoont heel wat 'bulten' en 'dalen'. Deze worden in eerste plaats veroorzaakt door evenwijdige gedeelten van de architektonische ruimte. Voor de frekwentiekarakteristiek van de ruimte zijn deze onregelmatigheden nefaster naarmate ze meer uitgesproken zijn. Zij kompromiteren de lineariteit van de ruimte. Zowat alle architekten zondigen bij de konceptie van akoestische ruimtes tegen de basisprincipes van een goede akoestiek:
Meestal wordt slechts het laatste punt berekend...
Wanneer we van deze kurve het gemiddelde berekenen (grafisch) dan vinden we de galmtijd van een ruimte (bij definitie) als dat punt op de tijdsas, waarbij de initiele geluidsdruk met 60dB (of, een faktor 1000) is gezakt. Voor rudimentaire praktische metingen van de galmtijd in relatief grote ruimtes kan een gekalibreerd (alarm)pistool worden gebruikt. Uiteraard moet de voortgebrachte geluidsdruk van het pistool voorzien van standaard patronen, bekend zijn. Het gebruik van een pistool berust akoestisch hierop, dat de knal spektraal gezien een erg breed spektrum heeft (alle frekwenties zijn erin vertegenwoordigd). Uit een analyse van het verloop van het spektrum in de tijd kan een goed beeld worden verkregen, niet alleen van de galm alleen, maar ook van de frekwentie lineariteit van de ruimte. Voor dergelijke analyse is steeds een komputer nodig evenals een nauwkeurige meetmikrofoon (Broel & Kjoer of Schoeps) en een digitaal opnametoestel.
De optimale galmtijd is een veel bediskuteerd onderwerp waarover de meningen niet helemaal op objektieve gegevens kunnen worden teruggevoerd. Een gangbaar overzicht van wenselijke galmtijden wordt gegeven in volgende grafiek:
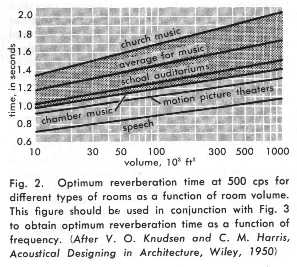
Merk vooral op dat naarmate verstaanbaarheid groter moet zijn, de galmtijd ook korter wordt genomen. Voor leslokalen en auditoria is 0.5 s een geschikte waarde. Diezelfde verstaanbaarheid is evenwel van kruciaal belang voor het analytisch horen en luisteren in het algemeen. Een grotere galmtijd neemt altijd detail weg in de waarnemingsmogelijkheden van het oor.
Voor progressieve hedendaagse muziek, waarbij groot belang wordt gehecht aan timbrale analyse en temporele precizie, is een korte galmtijd van groot belang. Slechte ensembles (en opnames) verdoezelen graag de vaak bedenkelijke kwaliteit van hun samenspel of zang, door een overmaat aan galm. Een 'dankbare' akoestiek heet dat dan...
Voor elektrisch versterkte muziek is galm eigenlijk steeds een ergerlijke kwaal. Ruimtes die daarvoor speciaal worden ingericht, moeten dan ook bij voorkeur zoveel mogelijk dempend worden gemaakt.
Galmtijden van enkele beroemde of beruchte ruimtes:
| PLAATS | VOLUME | GALMTIJD |
| Keulen, Dom | >100000 m3 | 13 sekonden |
| Milaan, Scala (Opera) | 1.5 sekonden | |
| Wenen, Redoutenzaal | 10000 m3 | 1.4 sekonden |
| Wenen, Musikverein | 15000 m3 | 2 sekonden |
| Boston, Symphony Hall | 18000 m3 | 1.8 sekonden |
| Rome, St.Pietersbasiliek | 3.5 sekonden | |
| Praag, theater | 6600 m3 | 1.3 sekonden |
| Festspielhaus, Bayreuth | 18000 m3 | 2.2 sekonden |
De idee een universele ('polyvalente') ruimte te kunnen bouwen -een idee dat onder meer aan de bazis lag van de oprichting van de 'kulturele centra' in elk vlaams boeregat- moet dan ook naar het rijk der waanideeen worden verwezen. De opgemeten galmtijden van de belangrijke koncertruimtes uit de 18e eeuw varieren zonder uitzondering tussen 1 en 1.3 sekonden. Barokmuziek, met haar typische ornamentiek, gaat inderdaad voor een goed deel verloren in grotere ruimtes en koncertzalen.
De galmtijd in een ruimte loopt niet gelijkmatig voor alle frekwenties. Over het algemeen wordt die ideale tijd, berekend of bepaald bij 500Hz, voor lagere frekwenties proportioneel verlengd, zodat deze bij 100 Hz 1.5 x de galmtijd bij 500Hz bedraagt. Vanaf 500Hz moet de galmtijd echter zoveel mogelijk frekwentieonafhankelijk verlopen. Een veel gehanteerde kurve voor de lage-tonen korrektie van de galmtijd wordt gegeven in volgende grafiek:
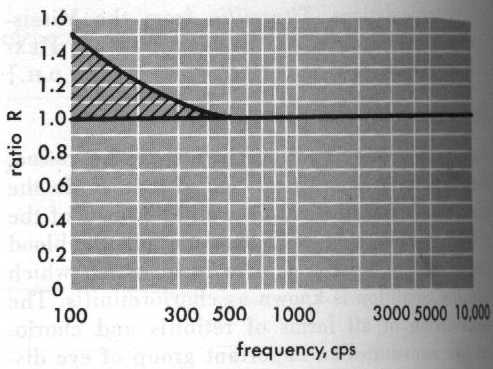
Een aspekt dat ook vaak uit het oog wordt verloren, is de demping van het geluid als gevolg van de samenstelling van de lucht. De belangrijkste faktor hier is de relatieve luchtvochtigheid. Het merkwaardige hiermee is dat deze demping ook weer een niet lineaire funktie blijkt te zijn van de frekwentie en dat ze meer uitgesproken wordt naarmate de toonhoogte stijgt. Volgende grafiek moge dit duidelijk maken:
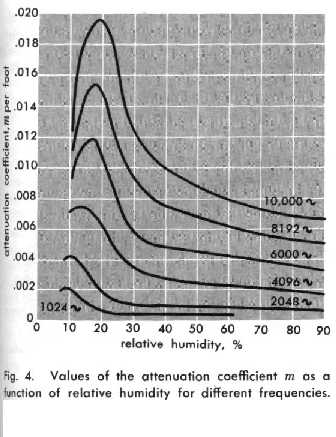
Vanaf toonhoogtes van ca. 2kHz moet hiermee rekening worden gehouden. Bij ultrasoon is dit zelfs bijzonder uitgesproken: wanneer de demping tot -3dB bij 20kHz ligt op 10 meter, dan wordt dit voor 50kHz nog slechts 3 meter en voor 100kHz, 2 meter.
Een formule voor het berekenen van de demping ziet eruit als:
D = 20
log L + dL
L is hierin de afstand tot de geluidsbron in meters. De waarde voor d (m in de hierboven afgedrukte grafiek, die bovendien in antieke voeten in opgesteld...) is 0.6dB/m bij 20kHz, 2dB/m at 50kHz and 3dB/m at 100kHz. D is de demping in dB.
De luchtvochtigheidsfaktor is vandaag slechts zelden een erg veranderlijke parameter in gebruikelijke akoestische koncertzalen: airconditioning stabiliseert er zowel temperatuur als vochtigheid. Waar evenwel massaal veel publiek samenkomt, kan deze faktor wel degelijk de akoestische eigenschappen van de ruimte beinvloeden. In openlucht kan het verschijnsel bijzonder goed waargenomen worden: bij zware mist (de relatieve vochtigheid bereikt dan bijna het verzadigingspeil van 100%) horen we in openlucht heel wat minder omgevingsgeluid dan bij droog en helder weer, een verschijnsel dat mede heeft bijgedragen tot heel wat ongevallen in de scheepvaart op zee.
Voor de akoestische berekening van ruimtes wordt -bij een eenvoudige benadering- vaak uitgegaan van de gemiddelde door het geluid afgelegde weg, dus de gemiddelde afstand van de geluidsbron tot de wanden waardoor het geluid kan worden weerkaatst. Een eenvoudige gebruiksformule voor het bepalen van deze gemiddelde vrije weg in funktie van het volume van een ruimte is:
w = 4 V / S
waarin V= volume van de ruimte in kubieke meter, en S=totale oppervlakte van de ruimte.
Het aantal reflekties van geluidsgolven per tijdseenheid is
r = v S / 4 V
, waarin v= geluidssnelheid in m/s, S en V zoals hiervoor. Bij elke reflektie neemt de intensiteit van de geluidsgolf een beetje af, waarbij het verschil geabsorbeerd wordt door het reflekterend oppervlak. Noemen we nu a de absorbtiecoefficient, dan is 1 - a de hoeveelheid gereflekteerd geluid. De absorbtiecoefficient voor een gegeven ruimte kan experimenteel of analytisch worden bepaald en wordt berekend als:
a = (a1.S1 + a2.S2 + a3.S3 + .... ) / (S1 + S2 + S3...)
waarin S1, S2... de oppervlaktes zijn van de reflekterende wanden en a1, a2... de absorbtiecoefficienten voor deze respektievelijke wanden. De waarden daarvan hangen af van de gebruikte materialen en kunnen worden weergevonden in tabellen voor bouwmaterialen. Ter illustratie geven we voor enkele materialen enkele waarden:
| Frekwentie | ||||||
| materiaal | 125Hz | 250Hz | 500Hz | 1000Hz | 2000Hz | 4000Hz |
| Marmer | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 | 0.02 |
| baksteenmuur | 0.01 | 0.01 | 0.02 | 0.02 | 0.02 | 0.03 |
| houten vloer | 0.15 | 0.11 | 0.10 | 0.07 | 0.06 | 0.07 |
| multiplex panelen op lattenraster | 0.6 | 0.3 | 0.1 | 0.09 | 0.09 | 0.09 |
| pleister | 0.3 | 0.15 | 0.1 | 0.05 | 0.04 | 0.05 |
| tapijt op vilt | 0.08 | 0.27 | 0.39 | 0.34 | 0.48 | 0.63 |
| dikke gordijnen tegen muur | 0.14 | 0.35 | 0.55 | 0.72 | 0.7 | 0.66 |
| rietvezeltegels op beton | 0.22 | 0.47 | 0.7 | 0.77 | 0.7 | 0.48 |
Nu weten we dat de geluidsdruk evenredig is met de vierkantswortel uit de geluidssterkte, waardoor we de gemiddelde afname van de geluidsdruk per reflektie kunnen berekenen als:
gf = 10 log( 1/(1-a))
, in dB per reflektie. Noteer dat absorbsiekoefficienten steeds genormalizeerd zijn, d.w.z. hun waarde is begrepen in het interval 0 tot 1.
De Noord-Amerikaanse fysikus Wallace Clement Sabine (1863-1919) bestudeerde in de jaren 1895 tot 1905 grondig en systematisch de akoestiek van architekturale ruimtes en kwam zo tot volgende (niet erg precieze) formule waarmee de galmtijd van een ruimte kan worden berekend:
t = 0.16 V / S
(waarin t is uitgedrukt in sekonden, V in kubieke meter en S in vierkante meter). De waarde voor S slaat hier op de akoestisch effektieve oppervlakte van alle absorberende grensvlakken van de beschouwde ruimte. De met deze formule berekende galmtijd is bijna steeds groter dan de empirisch bepaalde waarde. Voor niet-rechthoekige ruimtes is de formule trouwens volstrekt niet te gebruiken.
Tegenwoordig wordt dit onderzoek meestal uitgevoerd met komputersimulatoren, volledig in software dus. Deze laten immers toe een ruimte akoestisch te berekenen nog vooraleer ze werkelijk is gebouwd. Deze simulatoren zijn evenwel bijlange niet perfekt noch betrouwbaar, zodat een feitelijke empirische meting van de reeele akoestiek van een ruimte nog steeds het enige echt betrouwbare middel is voor akoestisch onderzoek van ruimtes.
Mechanische en architektonische maatregelen ter verandering van de akoestische eigenschappen van een ruimte
1.- Isolatie
a. kontaktgeluid: wordt overgebracht via trilling van materialen: Vloerdraagbalken, palen , wanden, vloerpanelen, tuikabels.
Een piano of een drumstel op een houten vloer zal een groot deel van de voortgebrachte trillingen via de poten naar de vloer overbrengen en op die wijze naar het onderliggende lokaal overdragen. Het plafond daarvan fungeert dan als extra resonator. De enige goede remediering bestaat er in dergelijke gevallen in, een 'zwevende' vloer toe te passen: een vloerkonstruktie bovenop de bestaande die er als het ware op drijft (bvb. op olie) en in elk geval nergens mechanisch is verbonden met architekturale delen die zelf kunnen trillen. Dat bij dergelijke oplossing de kosten de pan uitswingen zal duidelijk zijn. Minimale remedieringen kunnen erin bestaan de piano op rubberen voetjes (trillingsdempers) te plaatsen of het drumstel op een zachte rubberen mat met een dikte van ca. 5cm.
Ook luidsprekers opgehangen aan zolderingen of wanden, geven een goed deel van hun trillingen via mechanisch kontakt door aan de belendende lokalen. Gebruik dan ook steeds elastisch materiaal (neopreen bvb.) voor bevestiging en ophanging.
b. akoestisch overgedragen geluid: via lucht kanalen en verbindingswegen. Deuren en ramen sluiten is natuurlijk de allereerste imperatief. Kieren zijn moeilijk te vermijden en laten heel wat geluid door. Daarom worden in akoestisch te isoleren lokalen steeds dubbele gepolsterde deuren en ramen toegepast. De afstand tussen de beide deur- of raamelementen moet daarbij minstens 15cm bedragen. Als algemene regel; voor akoestische isolatie geldt dat het beter is zoveel mogelijk materiaalovergangen in te lassen dan dik isolerend materiaal te gebruiken. Overigens is het gros van het beschikbaar isolatiemateriaal ontworpen voor termische isolatie en daarvoor gelden heel andere wetmatigheden dan voor geluid. Rotswol en piepschuim bvb. zijn slechte akoestische isolatoren ook al zijn hun termische isolatiewaarden uitstekend. Akoestische isolatie vergt steeds heel wat meer ruimte dan termische. Getuige hiervoor bvb. de toepassing van een U-vormig toegangssas in professionele geluidsopnamestudios.
2.- demping:
een selektieve demping van een smal frekwentiegebied kan worden bereikt met kaviteitsresonatoren in de reflekterende wanden. De kaviteitsresonatoren worden berekend als Helmholtz resonatoren en afgestemd op de de dempen frekwenties.
demping van hoge tonen kan via zachte oneffen materialen: gordijnen, tapijten
demping van lage tonen kan via grote elastische dunne reflekterende panelen. Licht multiplex of triplex is hiervoor erg geschikt. Dun polykarbonaat heeft het voordeel doorzichtig, elastisch, sterk en onbrandbaar te zijn.
Globale demping wordt bereikt door perforatie van de reflekterende wanden. Bekend zijn zeker de vierkante geperforeerde plafondtegels uit zachtboard. Tegenwoordig worden ze ook in kunststoffen gefabriceerd.
Het versterken van bepaalde (lage) frekwenties kan gebeuren door toepassing van golfpijpresonatoren, zoals o.m. toegepast in luidspreker basreflex kasten.
3.- reflektie en projektie:
koncentratie van geluid op een bepaald punt in de ruimte kan worden bereikt door toepassing van parabolische reflektoren. Deze techniek vind vooral toepassing bij de geluidsopname: de paraboolmikrofoon voor geluidsjagers. Militaire toepassingen -voor luchtafweergeschut- dateren van rond de eerste wereldoorlog. De laagste frekwentie waarvoor nog bundeling kan optreden is een funktie van de cirkelvormige doorsnede van de mond van de parabool.
dispersie en verspreiding van geluid over een breed gebied van de ruimte kan worden bereikt via hyperbolische reflektoren. We treffen die vaak aan in de vorm van verplaatsbare panelen opgesteld achter en/of boven symfonische orkesten in zalen met een allesbehalve ideale akoestiek voor dergelijk gebruik. (bvb. de mierezaal in de hoogpoort, de bijlokekoncertzaal...)
versterking van de geluidsdruk kan worden bereikt door toepassing van exponentiele hoornkonstrukties. Soms worden auditoria (gedeeltelijk) in een dergelijke vorm gebouwd. Vroeger werden exponentiele hoorns vaak gebruikt in bioskopen, waarbij de trechter van de hoorn onder het publiek doorliep en de mond het gehele oppervlak van het projektiescherm kon beslaan.
De galm van een ruimte kan worden verminderd door deuren en ramen te openen. Uiteraard neemt men daarbij tevens ook de akoestische isolatie weg...
4.- lineariteit
Bij het ontwerpen van de ruimte moeten parallelle wanden tot elke prijs worden vermeden. De ideaalste vorm voor het bereiken van een lineaire akoestiek is de tetraeder. De galmtijd is daarbij een funktie van de afmetingen en uiteraard van de reflektiekoefficient van de vlakken waaruit hij is opgebouwd.
Wanneer in een gegeven ruimte parallelle wanden aanwezig zijn, moet telkens een ervan niet-reflekterend worden gemaakt voor het frekwentiegebied waarbinnen staande golven kunnen optreden. Het aanbrengen van niet-evenwijdige panelen behoort ook tot de vaak toegepaste mogelijkheden.
Wanneer mechanische of architektonische maatregelen onmogelijk zijn of stoten op financiele of monumententechnische bezwaren, dan blijft ons als laatste redplank nog slechts het beroep op informatika en elektronika...
Elektronische ingrepen op het akoestisch gedrag van een ruimte
- frekwentie korrektie (equalising)
- uitmiddeling van het galmgedrag
- versterking met vertragingstijden
Het principiele probleem met dit soort oplossingen bestaat erin dat de ruimte gaat liegen: ze klinkt niet langer in overeenkomst met haar uitzicht en fysische parameters. Ook de lokalisatie van de deelgeluidsbronnen in een dergelijke zaal, onontbeerlijk voor een analytische beluistering van muziek, heeft onvermijdelijk zwaar te lijden onder dergelijke ingrepen. (vb: Bijloke zaal).
Synthetische galm en ruimte effekten
- analoge technieken:
- digitale technieken
zie boekdelen 1 en 2.
| Terug naar inhoudstafel kursus: <Index Kursus> | Naar homepage dr.Godfried-Willem RAES | Naar lesrooster akoestiek | Naar index boekdeel akoestiek |