De titel van deze suite is een knipoog naar de 'Proeven van Stijlstudie' van de Nederlandse komponist Jacob Van Domselaer. Algoritmische muziek bij uitstek zou men kunnen zeggen en ja, die aanpak is in mijn werk aanwezig vanaf het prille begin. Met de opkomst en beschikbaarheid van komputers nam het echter een hoge vlucht: denken we maar aan eerdere komposities zoals 'Power of tree', 'Fuzzy Harmony Studies', 'Book of Fugues', ' Jumpy Variations', 'Tropes', 'Four Saisons', 'Primes', 'Shifts', '2bv-2b'... Gedurende vele decennia vormde algoritmische kompositie ook een vast onderdeel van mijn kompositiekursus aan het Gentse Conservatorium, vandaag een departement van de 'School of Arts' aan Hogent. Vele komposities en schetsen daarvoor werden aanvankelijk uitgewerkt voor instrumentale bezettingen (bvb. 'Shifts' , 'Power of Tree', 'Primes', '2bv-2b' enz...), latere dan weer voor synthesizers en samplers ('Betapi', 'Four Saisons'...). Het robotorkest kreeg in de laatste decennia een grote boost waardoor we -soms ook met de hulp van enkele daarvoor betaalde medewerkers bij Stichting Logos- heel wat algoritmische experimenten konden uitwerken en realiseren. Voor de verklanking van enkele algoritmes maakten we gebruik van een -inmiddels onvindbaar geworden- site opgezet door de Zweedse komponist Daniel Cummerow in 1998. Hij gebruikte mappings gebaseerd op spelregels van Olivier Messiaen om de cijferreeksen van vele irrationale konstanten en reeksontwikkelingen 'muzikaal' te maken. Uit al dit materiaal en uiteraard een heleboel eigen en nieuw materiaal hebben we geput voor het samenstellen en orkestreren van deze nieuwe samenhangende suite. Het ligt in onze bedoeling deze objektief muzikale suite verder uit te breiden met een passende choreografie.
1.- Priemmaten [2'45"]
Continuo's opgebouwd met repeterende sekwensen uit delingen met priemgetallen, hier en daar onderbroken door irrationele -systeemvernietigende- maar abrupt afgebroken erupties ; eigenlijk overblijfselen van een orkestratiepoging van een vroegere medewerker. Omdat fouten ook vaak systeemverhelderend kunnen werken, lieten we ze -met wat wijzigingen- grotendeels staan. Deze mapping is ontleend aan de bestanden van Daniel Cummerow.
2.- Fraktalen en spiralen [2'25"]
Spiralen zijn van oudsher een van de meest dankbare en ook eenvoudigst wiskundig te berschrijven vormen voor onderwerping aan de algoritmiek eigen aan fraktalen van Mandelbrot e.a.
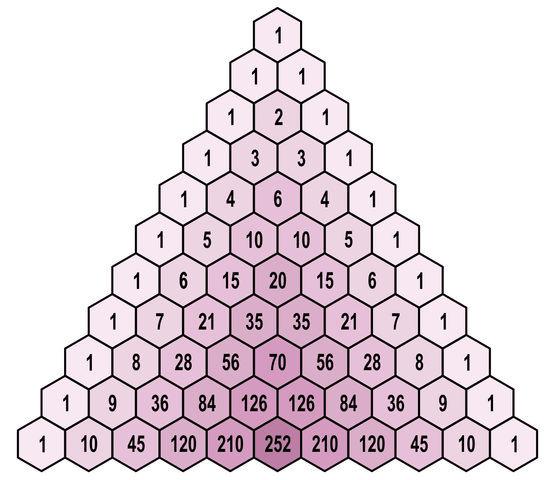
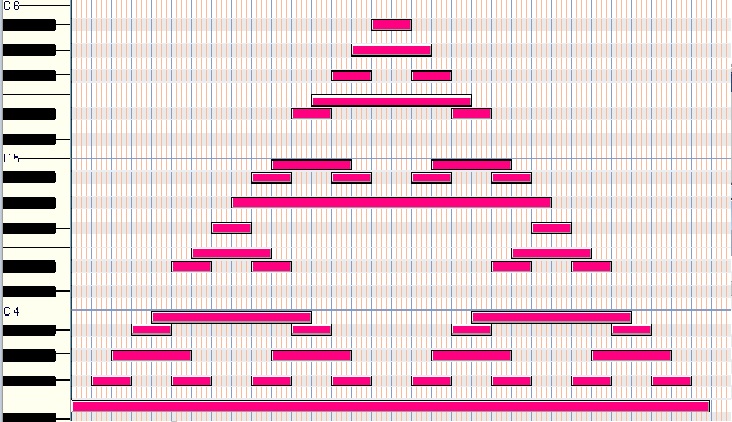
3.- Pascal's driehoek [2'20"] De driehoek van Pascal, een grafische weergave van de berekening van binomiaal koefficienten. Eigenlijk bedacht, lang voor Blaise Pascal (1623-1662), door Chinese wiskundigen.
In de driehoek komt de eigenschap tot uitdrukking dat elke binomiaalcoëfficiënt de som is van de twee bovenliggende. De getallen in de driehoek geven het aantal wegen aan vanaf de top naar de plaats van zo'n getal, waarmee ook de besproken eigenschap verklaard is. Omdat er steeds 2 keuzen zijn om de weg naar onder te vervolgen is de som van de getallen op een rij de overeenkomstige een macht van 2. De hier gebruikte mapping is afkomstig van Daniel Cummerow.
4.- Priemitief [3'15"]
Ook hier maakten we gebruik van een mapping van Daniel Cummerow.
5.- Pythagoras trios [1'30"] . Alle verzamelingen van drie gehele getallen a,b,c waarvoor geldt dat a^2 = b^2 + c^2. Op kleitabletten uit de tijd van Hammurabi komen al pythagorese drietallen voor. Op het tablet Plimpton 322 bijvoorbeeld staan 15 drietallen, waaronder (56,90,106), (119,120,169) en zelfs (12709,13500,18541). Men kende ook in India zulke getallen. In de Baudhayana-Sulbasutra uit de 6e eeuw v.Chr. staan vijf drietallen. Het eenvoudigste pythagorees drietal (3,4,5) is bekend om zijn toepassing voor het bepalen van een rechte hoek. Daartoe gebruikte men een rondlopend touw met 12 knopen op gelijke afstanden. [uit: Wikipedia] De hier gebruikte mapping komt van Daniel Cummerow.
6.- Priemair Gruis [3'48"] Een Daniel Cummerow mapping van de ontwikkeling van een deling met priemen op robots waarin het ruisaandeel in de klanken op de voorgrond komt.
7.- Niven getallen [1'50"] Niven getallen: (Ook Harshad getallen genaamd) zijn gehele getallen die deelbaar zijn door de som van digits waaruit ze bestaan. Harshadgetallen in talstelsel met grondtal n worden ook wel aangeduid als n-harshad- of n -nivengetallen. De naam nivengetal komt van I.M. Niven, die deze getallen beschreef in een bijdrage op een conferentie over getaltheorie in 1997. Het woord harshad is afgeleid van Sanskriet harsa, dat 'vreugde' betekent. Hier is het begin van de reeks Niven-getallen: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 18, 20, 21, 24, 27, 30, 36, 40, 42, 45, 48, 50, 54, 60, 63, 70, 72, 80, 81, 84, 90, 100, 102, 108, 110, 111, 112, 114, 117, 120, 126, 132, 133, 135, 140, 144, 150, 152, 153, 156, 162, 171, 180, 190, 192, 195, 198, 200, ...
8.- Copeland-Erdös versus Froda [2'03"] Het Copeland-Erdos irrationaal getal is opgebouwd als 0, met na de komma alle priemgetallen in volgorde. De Frodo konstante is 2^e
9.- Lorenz Vlinder [2'17"] Lorenz butterfly: eerste afgeleiden naar de tijd van 3-dimensionele funkties dx/dt, dy/dt, dz/dt waarmee chaotische verschijnselen beschreven worden.
De Lorenz-attractor van Edward Lorenz in een driedimensionale faseruimte. De bijbehorende differentiaalvergelijkingen beschrijven een eenvoudig meteorologisch model. Het systeem beweegt langs de getoonde banen links met de klok mee, na oversteek rechts tegen de klok in, na oversteek links...enzovoorts. Bij elke omloop verbreedt de band van de banen zich. De figuur is berekend met de standaard parameters r=28, s = 10, b = 8/3 (of 2.666667). [bron: Wikipedia]
10.- Fourier [1'30"] Een spektraaltransformatie volgens Neko.
11.- Sierpinski's driehoek [2'16"] De driehoek van Sierpinski is een fractaal die werd ontdekt door de Poolse wiskundige Waclaw Sierpinski. Uit een gelijkzijdige driehoek wordt de driehoek verwijderd die gevormd wordt door de middens van de drie zijden. Vervolgens wordt deze procedure herhaald in elk van de drie overgebleven driehoeken. Deze muzikale uitwerking maakt gebruik van de
kwarttoons robots <Qt>, <Xy> en <Puff>. Ook <Rodo> en <Spiro> kregen een bijrol toegewezen. De mapping wordt geheel duidelijk in deze pianorol weergave van de <Qt> partij: 12.- Euler's Phi [2'05"] In de getaltheorie is de indicator of totiënt van een positief natuurlijk getal n , genoteerd als f ( n ) \ Phi , het aantal positieve natuurlijke getallen kleiner dan of gelijk aan n die onderling ondeelbaar zijn met n . Zo is bijvoorbeeld f ( 8 ) = 4 , omdat van elk van de vier oneven getallen 1, 3, 5 en 7 de grootste gemene deler met 8 gelijk is aan 1, en die vier getallen daarom onderling ondeelbaar met 8 zijn. De indicator werd grondig bestudeerd door de Zwitserse wiskundige Leonhard Euler.
Dit is een grafiek van de eerste 100 waarden van de Euler-functie. De waarden op de bovenste lijn behoren bij de priemgetallen. In de hier gekozen mapping, pasten we over het gehele verloop een doorlopend accellerando toe.
13.- Fibonacci [3'24"] Fibonacci reeksen, hier gemapt op tempoverhoudingen. Elk instrument krijgt slechts een enkele noot toegewezen waardoor het muzikaal resultaat een minimalistisch karakter krijgt. .
De Fibonacci getalreeksen bestaan uit gehele getallen waarbij elk getal gelijk is aan de som van zijn twee voorgangers. 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, .... Fibonacci getallen werden al beschreven in Indische wiskundige teksten van Pingala daterend van 200 jaar voor onze tijdrekening. In die teksten worden mogelijke patronen besproken voor gedichten in het Sanskriet opgebouwd uit syllaben van twee verschillende lengtes. Wij kennen ze als Fibonacci reeksen genoemd naar de Italiaanse wiskundige Leonardo di Pisa, die ook Fibonacci werd genoemd en die de reeks behandelde in zijn boek uit 1202.
14.- Amigo [1'20"] Amigo: w(1) en 1/w(1), een funktie en de omkering ervan
15.- e [3'06"] basisgetal van de natuurlijke logaritmen. De formule voor de berekening van dit irrationaal getal is
. Wanneer we een lus programmeren voor almaar toenemende waarden van x, dan groeien de cijfers na de komma alsmaar verder aan, wat een boeiende muzikale lijn kan opleveren. Anders dan bij rationale getallen, krijgen we hier helemaal geen repeterende patronen. De mapping op modi ontleend aan Olivier Messiaen zorgt hier wel voor een bijzondere harmonische sfeer waarin de modale geur van Messiaen duidelijk aanwezig is.
16.- Pi [2'06"], een nieuwe versie van 'Flodders' het tweede deel uit mijn 4e symfonie. Ook hier weer gekenmerkt door een grillig, welhaast jazzy, tema afgeleid van de cijferreeks van het getal Pi. Deze mappings ontleenden we aan Daniel Cummerow. Een van de bekendste reeksonwikkelingen voor de berekening van pi is die van mijn voornaam-genoot Gottfried-Wilhelm Leibniz: pi=(4/1) - (4/3) + (4/5) - (4/7) + (4/9) - (4/11) + (4/13) - (4/15) ... Maar, er zijn bijzonder veel alternatieve en ook heel wat snellere reeksontwikkelingen bekend. Zo bijvoorbeeld deze, geplukt uit Wikipedia: :
Een heleboel decimalen vinden we hier:
Net zoals bij e, krijgen we hier nooit repeterende patronen te zien.
17. Fraktaal [2'07"] . Hoewel ze vandaag wat op de achtergrond zijn geraakt waren allerhande fraktalen een ware hype in de jaren '80 van vorige eeuw. De theorievorming errond door wiskundigen zoals Benoit Mandelbrot is daar niet vreemd aan. De komplekse fraktale figuren die we hier in muziek omzetten vertonen heel wat gelijkenis met sneeuwkristallen. De hier toegepaste mapping regels werden bedacht door Robert Walker in 2001. Ze berusten op een Fourier spektrale reeks.
18. Turpel reeks [1'45"] , een getallen sekwens ontleend aan de OEIS.
19. Ramajunan getal [2'36"] : Het merkwaardige aan de reeksontwikkeling voorgesteld door de Indische wiskundige Ramanujan is dat hij beide irrationale getallen Pi en e in een enkele formule samenbrengt. Dat deed Euler natuurlijk ook met zijn beroemde e^Pi.i = -1, maar dat was dan wel heel wat later.
Dit levert als beginsekwens op: 2.06636567706... Het Ramajunan getal -1729- is het kleinste getal dat kan voorgesteld worden als de som van twee kwadraten: 1729=1^3+12^3=9^3+10^3. De in deze proeven gebruikte modale mapping gebruikt de noten C, G, Db, Ab, met een toegevoegde F, overeenkomstig het merkwaardige getal 1728, dat de derde macht is van 12. Dat getal in het twaalftallig stelsel wordt geschreven als 1000. Verder is het deelbaar door 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 32, 36, 48, 54, 64, 72, 96, 108, 144, 102, 216, 288, 432, 576, 864 en zichzelf.
20. SixSpek: [2'48"] Deze proeve gaat terug op een algoritme dat we ontwikkelden in 1996 voor het berekenen van zesstemmig kontrapunt volledig gebaseerd op spektrale harmonie. Toen was het niet meer dan een test-bestandje gemaakt om het programma van bugs te ontdoen. In 2024 namen we de kode en het bestand opnieuw ter hand en gebruikten we het als eerste -maar voorlopig- sluitstuk voor onze Proeven van Wiskunst.
21. StokFrak [1'26"] : Stochastisch gevarieerde fraktale wolkjes, uitgaand van een reeksontwikkeling op midi-getallen gemapt door Robert Walker in 2001. In de orchestratie van deze proeve wordt vooral de allerhoogste tessituur van het robotorkest gebruikt. De stochastische behandeling van de fraktale strukturen sluit een knipoog in, als eerbetoon aan Iannis Xenakis, aan wiens algoritmische benadering van de muziek we veel verschuldigd zijn. De duur is beperkt tot anderhalve minuut..
De verschillende delen van deze suite kunnen en mogen ook afzonderlijk uitgevoerd worden. Ook de volgorde mag naar eigen inzicht en keus bepaald worden.
Gedeeltelijke Premiere: 15 augustus 2024, 20u00 : Logos Tetraeder Gent. (een reeks van 10 studies).
Uitvoering tweede reeks: 18 september 2024, 20u00: Logos Tetraeder Gent. (6 studies)
Uitvoering derde reeks: 24 oktober 2024, 20u00: Logos Tetraeder (5 studies)
The scores may undergo some minor changes and updates in the near future.
Bibliografie:
Artur Portnoy, 'The mathematics of Music and Art', ed. Springer 2024
OEIS: The online encyclopedia of integer sequences ( https://oeis.org )
Clifford A.Pickover, 'Het Wiskunde boek', ed.Librero, na 2008, ongedateerd.