Clarinet acoustics: an introduction

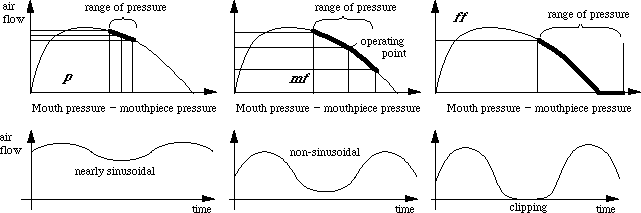
As we play more loudly, we increase the pressure (which moves the operating point to the right) and we also increase the range of pressure. This means that the (larger) section of the curve we use is no longer approximately linear. This produces an asymmetric oscillation. It is no longer a sine wave, so its spectrum has more higher harmonics. (Centre diagram.)

When we blow even harder, the valve closes for part of the part of the cycle when the pressure in the mouthpiece is low due to the standing wave inside the instrument. So the flow is zero for part of the cycle. The resultant waveform is 'clipped' on one side (diagram at right), and contains even more high harmonics. As well as making the timbre brighter, adding more harmonics makes the sound louder as well, because the higher harmonics fall in the frequency range where our hearing is most senstitive (See What is a decibel? for details). Conversely, playing in the linear range of this playing curve gives few high harmonics, so the minimum playing level of the clarinet can be very quiet indeed, a feature often used by composers.

While talking about decibels, we should mention that spectra, including those on our clarinet site are usually shown on a decibel scale. This means that one notices easily on the spectrum a harmonic that is say 20 dB weaker than the fundamental, even though it has 10 times less pressure and 100 times less power. What is important is that your ear notices it too, because of the frequency dependence referred to above. However, it is much more difficult to notice the presence of harmonics if you look at the waveform.

The clarinet is a 'closed' pipe

The behaviour of closed and open pipes are explained in Open vs closed pipes (Flutes vs clarinets), which gives more explanation of this animation.

For the purposes of this simple introduction to clarinet acoustics, we shall now make some serious approximations. First, we shall pretend that it is a simple cylindrical pipe---in other words we shall assume that all holes are closed (down to a certain point, at least), that the bore is cylindrical, and that the mouthpiece end is completely closed. This is a crude approximation, but it preserves much of the essential physics, and it is easier to discuss. (We look at many of the complications in turn below and when explaining the real results.)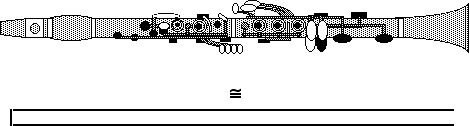

The natural vibrations of the air in the clarinet, the ones that cause it to play notes, are due to standing waves. (If you need an introduction to this important concept, see standing waves.) What are the standing waves that are possible in such a tube?

The fact that the clarinet is open to the air at the far end means that the total pressure at that end of the pipe must be approximately atmospheric pressure. In other words, the acoustic pressure (the variation in pressure due to sound waves) is zero. The mouthpiece end, on the other hand, can have a maximum variation in pressure. Now the distance between a zero and a maximum on a sine wave is one quarter of a wavelength. So, the longest standing wave that can satisfy these conditions is one that has a wavelength four times the length of the instrument, as shown at the top of the next figure: it has zero pressure at the open end (called a pressure node). Inside the tube, the pressure need not be atmospheric, and indeed the maximum variation in pressure (the pressure anti-node) occurs in the mouthpiece. The standing wave is sketched below. The bold line is the variation in pressure, and the fine line represents the displacement or the amplitude of the vibration of the air molecules. The displacement curve has an anti-node at the bell: air molecules are free to move in and out at the bell but, in the approximation where the mouthpiece is closed, there is little acoustic flow in the mouthpiece. (There is of course DC flow, but that does not affect the standing waves directly.)

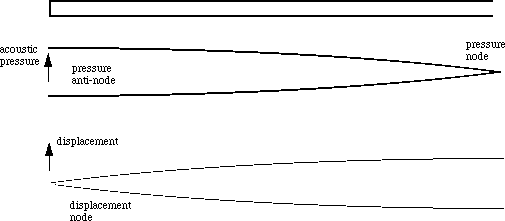
The frequency equals the wave speed divided by the wavelength, so this longest wave corresponds to the lowest note on the instrument: D3 on a Bb clarinet. (See standard note names, and remember that clarinets are transposing instruments, so that D3 is written as E3 for the Bb clarinet. Hereafter we refer only to the written pitch.) You might want to measure the length of your instrument, take v = 350 m/s for sound in warm, moist air, and calculate the expected frequency. Then check the answer in the note table. (You will find that the answer is only approximate, because of end corrections.)

You can play (written) E3 with this fingering, but you can also play other notes by overblowing--by changing your embouchure and changing the blowing pressure. These other notes correspond to the shorter wavelength standing waves that are possible, subject to the condition that the sound pressure be zero at the bell and a maximum in the mouthpiece. The first three of these (solid lines) are shown in the diagram below.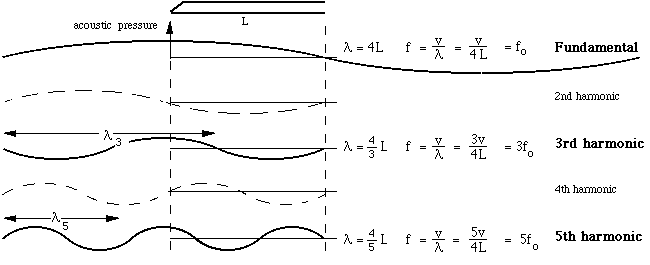

These three notes are approximately members of the harmonic series. Notes with these frequencies have the (written) pitches shown below. The complete harmonic series has the frequencies f_o, 2f_o, 3f_o, 4f_o, 5f_o etc. The clarinet, under these conditions, plays (approximately) the odd members of the series only. The missing even harmonics and their waves are shown in dashed lines and in parentheses in the diagrams. (You might like to compare this with the analogous diagram for the flute, which has all harmonics present.) There is also a more detailed discussion of the harmonic series of open and closed pipes.

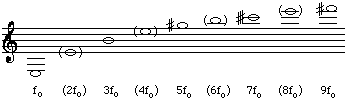
Harmonics of the lowest note on a clarinet.           Recording of notes played using only the fingering for the lowest note.

The notes in the diagram are the harmonics of the fundamental. The notes in the sound file are those played by overblowing, without using register keys (which is one reason why they don't sound pretty and don't start cleanly). You will observe that the played notes are successively flatter than the harmonic frequencies. The third is slightly flatter than B4, the fifth is about a semitone flat, the seventh more flat again. This is due to effects of the reed (itself a deformable element approximately in parallel with the bore) and effects of the bell (longer wavelengths penetrate less into the bell before being reflected.)

How the reed and pipe work together

When the clarinet is playing, the reed is vibrating at one particular frequency. But, especially if the vibration is large, as it is when playing loudly, it generates harmonics (see What is a sound spectrum?). The reed vibration tends to have both odd and even harmonics. However, in the low registers at least, only the odd harmonics set up, and are in turn reinforced by, standing waves. Consequently, the sound spectrum in the low registers has strong first and third harmonics, but weak second and fourth.

Spectrum and registers of the clarinet

Opening tone holes

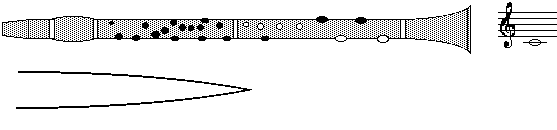
Observe that this note, which uses only a little more than half of the length of the clarinet, is still lower than the lowest note on a flute. (For a Bb clarinet, written C4 = sounding Bb3, the lowest note on a flute is B3 or C4.) This is one of the big advantages of a closed pipe: you get low notes with a shorter pipe.

For the moment, we can say the an open tone hole is almost like a 'short circuit' to the outside air, so the first open tone hole acts approximately as though the clarinet were 'sawn off' near the location of the tone hole. This approximation is crude, and in practice the wave extends somewhat beyond the first open tone hole: an end effect.

(For the technically minded, we could continue the electrical analogy by saying that the air in the open tone hole has inertia and is therefore actually more like a low value inductance. The impedance of an inductor in electricity, or an inertance in acoustics, is proportional to frequency. So the tone hole behaves more like a short circuit at low frequencies than at high. This leads to the possibility of cross fingering, which we have studied in more detail in classical and baroque flutes.)

The frequency dependence of this end effect means that the low note played with a particular fingering has a smaller end effect than does the corresponding note in the next register. If the clarinet really were a perfect cylinder with tone holes, then the registers would be out of tune: the intervals would be too narrow. This effect is removed by variations or perturbations of the cylindrical shape, including the shape of the mouthpiece, an enlarging of the upper region of the bore, and a gradual flare in the bottom half of the instrument, leading to the bell.

Register holes

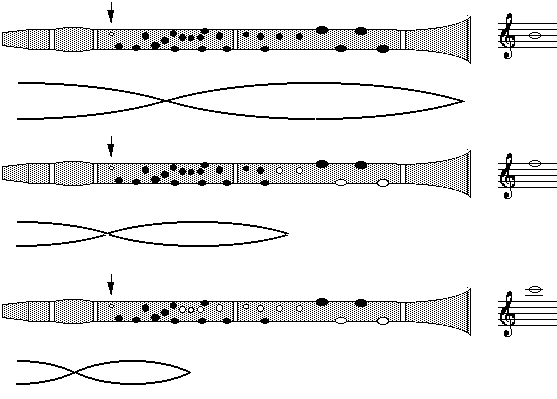
We mention in passing that the saxophone has two dedicated register holes for the second register and an automated mechanism that allows only one key to operate the hole appropriate to each end of the range. Multiple register keys have been tried on the clarinet, but have never become popular.

The speaker key is the register key used for the second register. In higher registers, other register holes are used: the altissimo register uses the hole that is normally closed by the index finger of the left hand. This hole is designed primarily as a tone hole, so it is bigger than it need or should be for an ideal register hole. This defect is not so important because it is used only for high frequencies, where its inertance is large. However some players partly cover this hole (half-holing) when using it as a register hole.

Let us open an aside to answer a question that has been asked a few times: "If the speaker key destroys the first resonance, but none of the others, why is it that the sound spectrum in the clarino register has only harmonics 3, 6, 9 etc? What happened to the fifth harmonic?" One can verify the basis of this question by looking at the spectra for E3 and B4.

When we play E3, the reed vibrates at the frequency of E3 (about 147 Hz for a Bb clarinet). In a steady vibration, only harmonics (odd or even) of this frequency are possible, and they are exactly harmonic. (See How harmonic are harmonics?.) The odd harmonics are supported by the resonances of the bore, and so the resultant sound spectrum is rich in odd harmonics but has weaker even harmonics, at least at low frequencies. (See How the reed and pipe work together.)

When we play B4, the reed vibrates at the frequency for this note (about 440 Hz for a Bb clarinet), which is three times the frequency of E3. Again, in steady vibration only harmonics (odd or even) of this frequency are possible. The fifth resonance of E3 (approximately G#5) is still present, as the impedance spectrum for B4 shows, but there is nothing to put energy into a vibration at that frequency.

Observe also that we are now in the clarino register (about which see the general comments on the page for B4). The resonances that one might have expected to support the 3rd and 5th harmonics of B4---ie the 9th and 15th harmonics of E3---are not close enough in frequency to be of any help. However, the acoustic response of the clarinet is strong enough to help all of the harmonics of the reed to some extent, and the resultant sound spectrum has no strong differences between even and odd harmonics.

We return to discuss register holes in more detail below, after we have discused the frequency response.

Cross fingering

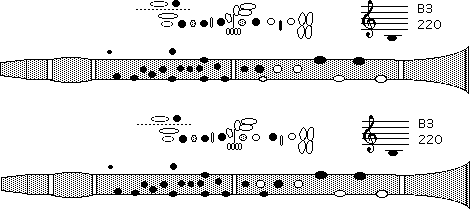
An open tone hole connects the bore to the air outside, whose acoustic pressure is approximately zero. But the connection is not a 'short circuit': the air in and near the tone hole has mass and requires a force to be moved. So the pressure inside the bore under a tone hole is not at zero acoustic pressure, and so the standing wave in the instrument extends a little way past the first open tone hole. (There's more about this effect under Cut-off frequencies.) Closing a downstream hole extends the standing wave even further and so increases the effective length of the instrument for that fingering, which makes the resonant frequencies lower and the pitch flatter.

The effect of cross fingerings is frequency dependent. The extent of the standing wave beyond an open hole increases with the frequency, especially for small holes, because it takes more force to move the air in the tone hole at high frequencies. This has the effect of making the effective length of the bore increase with increasing frequency. As a result, the resonances at higher frequencies tend to become flatter than strict harmonic ratios. Because of this, often one cannot use the same cross fingerings in two different registers.

A further effect of the disturbed harmonic ratios of the maxima in impedance is that the harmonics that sound when a low note is played will not 'receive much help' from resonances in the instrument. (Technically, the bore does not provide feedback for the reed at that frequency, and nor does it provide impedance matching, so less of the high harmonics are present in the reed motion and they are also less efficiently radiated as sound. See Frequency response and acoustic impedance. To be technical, there is also less of the mode locking that occurs due to the non-linear vibration of the reed.) As a result, cross fingerings in general are less loud and have darker or more mellow timbre than do the notes on either side. You will also see that the impedance spectrum is more complicated for cross fingerings than for simple fingerings, especially in the region around 1.3 to 2 kHz.

We have studied cross fingerings more extensively on flutes than on clarinets, by comparing baroque, classical and modern instruments. (We have not yet studied a chalumeau or classical clarinet to compare with the modern instrument.) See cross fingering on flutes or download a scientific paper about crossfingering.

Other effects of the reed

Cut-off frequencies

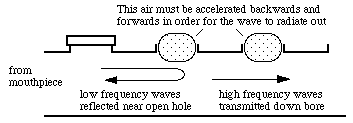
So high frequency waves are impeded by the air in the tone hole: it doesn't 'look so open' to them as it does to the waves of low frequency. Low frequency waves are reflected at the first open tone hole, higher frequency waves travel further (which can allow cross fingering) and sufficiently high frequency waves travel down the tube past the open holes. Thus an array of open tone holes acts as a high pass filter: some thing that lets high frequencies pass but rejects low frequencies. (See filter examples.) This is one of the things that limits the ability to play high notes on the clarinet. The stiffness of the reed is another: a clarinet will only play notes with frequencies lower than the natural frequency of the reed.

The player can alter the cut-off frequency, and this is one of the effects used to achieve the spectacular glissando in the opening bars of Gershwin's Rhapsody in Blue. The player begins by gradually sliding the fingers off the tone holes, with the principal effect of changing smoothly the end effect at the open tone hole, and so the pitch. This provides most of the glissando up to the thorat register. From this register up, the player changes the position and force of the lower lip on the reed, thereby changing its natural frequency and also uses the resonances in the vocal tract. Normally, the resonances of the instrument are so strong (have such high acoustic impedance--see below) compared with those of the vocal tract that the latter make only modest changes to the pitch. However, the player can reduce the strength of the instrument resonances by lowering the cut-off frequency below that of the note being played. To do this, the fingers are kept very near to the tone holes, partially covering them, so that the tone holes are effectively very small. In this state, the resonances of the vocal tract can be stronger than those of the instrument, so the note played tends to follow that of the tract resonances, which the player increases smoothly--with some considerable help from the change in the natural frequency of the reed as the player's bite changes simultaneously. There is a detailed discussion of these effects in this paper.

There is a more detailed explanation of cut-off frequencies and their effects here.

Frequency response and acoustic impedance of the clarinet

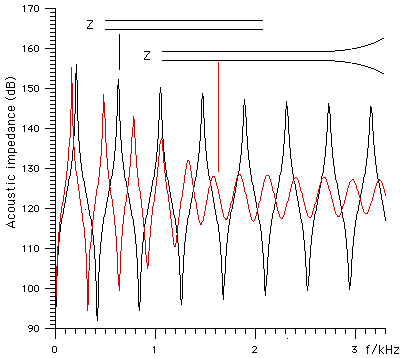
This figure shows in black the calculated impedance spectrum for a simple cylinder (the impedance is given in decibels: 20 log₁₀(Z/Pa.s.m^-3). A suitable reed attached to the input of this tube would play near the frequencies of the peaks, which are in the ratios of the odd harmonics 1:3:5:7 etc (see open and closed pipes for more explanation, and/or compare with the comparable curves for a saxophone). The curve in red is for the same cylinder, with a simple bell at the end. Note that the bell makes the pipe longer, so each peak and trough has been moved to lower frequencies, as expected. Note however the change in the overal shape: all of the resonances are now weaker (extrema are smaller). This is because the bell helps the sound waves in the bore to radiate out into the air. (Incidentally, the presence of a large, effective bell is what makes brass instruments loud: try playing a trombone with the tuning slide taken off.) More sound radiated means less sound reflected, so the standing waves are weaker.

This effect is less noticeable at low frequencies: the first maximum and minimum are not weakened very much, because the bell is much smaller than the wavelengths of the low frequency waves, and so is not very effective at radiating these waves. (Incidentally, this frequency dependent effect of the bell is what makes brass instruments brassy: the bell-less trombone has a sound that is darker, as well as softer.)

The effect of the bell is that of a high pass filter: it allows high frequencies to radiate out of the instrument, rather than reflecting back up the bore to help establish the standing wave. In this, it acts much like the cut-off frequency effect of the tone holes. In fact, one purpose of the clarinet's bell chiefly is primarily to provide a high pass filter for the lowest few notes, so that they have a cut-off frequency and so behave more similarly to the notes produced with several tone holes open.

We could state this another way: for all of the notes on a clarinet except the lowest few in the chalumeau and clarino registers, the array of open tone holes acts as a high pass filter. For the few notes mentioned, however, few or no tone holes are open, so the reflection condition is different, and so a purely cylindrical clarinet would have a noticeably different timbre for these few notes. So the bell performs a similar function for these notes. At frequencies well above the cut-off, the bell has other functions, including directional radiation of high frequencies.

So that is one reason why the clarinet departs from its approximately cylindrical shape for the last few tone holes. It is also non-cylindrical for a few centimetres at the other end. Which brings us to the effect of the mouthpiece.

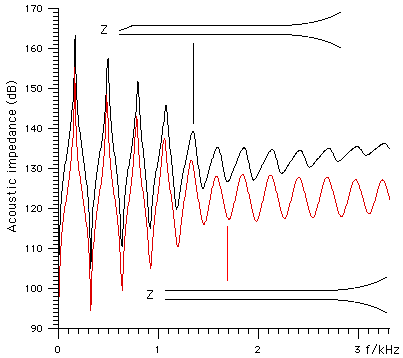
Here, the red curve is the same as the one we saw above: that for a cylinder with a bell. Now the black curve is for a cylinder plus a bell plus a conical constriction at the opposite end, which has approximately the same effect as a mouthpiece: it reduces the cross sectional area of the bore gradually as it approaches the reed. This has several effects.

First, it raises the impedance overall. This is because it functions like a horn or an impedance matching transformer, connecting a small area (where the same flow would require more pressure and therefore high impedance) to a large area.

Second, it does this more effectively at high frequency for maxima (all of which are shifted by 8-10 dB) than for minima (where the high frequency minima are much less deep than are the low frequency minima). This however is not important to the clarinet, because it operates at maxima, but is an important consideration in the design of flutes.

Third, it makes the peaks and troughs asymmetric. At high frequencies, the minima move to lower frequencies while the maxima occur at higher frequencies.

Of course the bore is not exactly cylindrical: there are local variations in radius, particularly near the barrel. The effects of these are to make subtle differences to the relative tuning of the registers.

Vocal tract effects

The effect of reed hardness

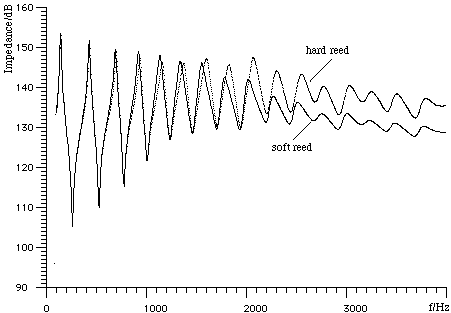
On this figure, the single dots are the experimentally measured impedance spectrum for E3, with a value of the compliance corresponding to a hard reed. The continuous line (actually the experimental points joined together) shows the spectrum for a soft reed. At low frequencies, there is not much difference, but you can already see a slight difference in frequency: the hard reed plays sharper, all else equal. As you go to higher frequencies, you see that the soft reed gives lower peaks. Lower peaks are harder to play, so the hard reed makes it easier to play high notes. (Unfortunately, a hard reed also makes it easier to play squeaks.)

To understand more about the detailed shape of these impedance curves, see the discussion of the experimental results for E3.

More about register holes

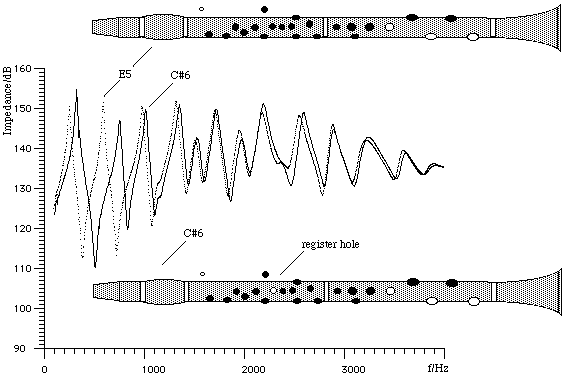
At low frequencies, however, the effect is greater, and this register hole substantially reduces the height of the second maximum. It also raises its frequency, and takes it out of the harmonic series with other peaks. These effects, especially the former, make the second peak harder to play, and so (provided you use the appropriate embouchure), the instrument will play the third maximum, which is C#6.

We have not mentioned the first maximum. It has already been weakened and shifted by the speaker key, which is open here. However, its maximum is not all that weak and a careless embouchure and low blowing pressure could find you dropping down to a muffled low note near that frequency. Further, the fourth peak is pretty high, too. With a hard reed and blowing hard, there's a danger of jumping up to this note, too. Which is why the altissimo register is hard to play. (There is more discussion of the altissimo register on the experimental page for C#6).

More detailed information

Now it's time to look at the set of measured impedance spectra and relate them to the sounds and sound spectra produced. Go to clarinet acoustics and click on the names of the notes.

Scientific papers on the clarinet

We have recently published two conference papers concerning the influence of the player's vocal tract on the pitch and timbre of wind instruments:

• Chen, J.M., Smith J. and Wolfe, J. (2009) "Pitch bending and glissandi on the clarinet: roles of the vocal tract and partial tone hole closure" J. Acoust. Soc. America, 126, 1511-1520.
• Dickens, P., France, R., Smith,. J. and Wolfe, J. (2007) "Clarinet acoustics: introducing a compendium of impedance and sound spectra". Acoustics Australia, 35, 17-24.
• Fritz, C. and Wolfe, J. (2005) "How do clarinet players adjust the resonances of their vocal tracts for different playing effects?", J. Acoust. Soc. America 118, 3306-3315.
• Fritz, C., Wolfe, J., Kergomard, J. and Caussé, R. (2003) "Playing frequency shift due to the interaction between the vocal tract of the musician and the clarinet". Proc. Stockholm Music Acoustics Conference (SMAC 03), (R. Bresin, ed) Stockholm, Sweden. 263-266.