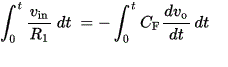The experimental legacy
in avoidance of integral calculus and differential equations
Godfried-Willem Raes
postdoctoral researcher
Orpheus Institute & Logos Foundation
2015
As we wanted this collection of music related articles focussed on electronics, readable and of practical use to musicians with some practical sense of kinds, we did our utmost best to avoid compex mathematics throughout these texts. But next to this point of departure, there is also a philosophical argument that can be brought in here: finitism. What makes higher math so inaccessible to most people is the introduction of integral calculus. Now, integral calcullus is entirelly based on reduction to infinity. Reality though, and certainly the reality of circuit design and electronics, confronts us just about anywhere with finite bounds: can you image a voltage ranging from -infinity to +infinity? The concept alone is deadly... Or, a resistance at 0 Ohms, an insulator that's perfect (infinite resistance), an interval of an infinite small amount... none of these concepts belong to the practice of electronics. Moreover, no resistor is perfect as it invariably will show up some capacitance and inductance. Neither can its value be considered to be a rock solid constant, as it may vary over time, with temperature and with load conditions and with humidity and air pressure. The same holds for capacitors: the insulation is not perfect and thus it will have a resistance (if it were perfect, it could withstand an infinite voltage and charge... just imagine). Due to the construction, it will have inductance as well. Last but not least in this list of passive components, we have coils -inductors- that allways have resistance as well as capacitance. Formulas that only have validity for platonic 'ideal' components are an amusement for theoretical physics and mathematics, but serve no practical purpose at all. Morover, they lead to misunderstandings and many design errors. Never trust God when it is allowed to enter the world of engineering.
All problems in electronics can be solved without the introduction of infinity.
A simple textbook integrator circuit (cfr. wikipedia: op amp integrator article) invariably presents us with an integral.
Although as we know, this calculates the surface of a curve for a variable over a time interval t, for an input resistor R1 and a feedback capacitor Cf with an input voltage vin and output voltage vo it's an unneeded introduction of infinity. Yet for not a single practical circuit this is even a bit usefull. The only thing we have to know when designing integrators, is that they are fundamentally low pass filters. Their -3dB limit being defined and calculated as fc = 1 / 2.Pi.Rf.Cf and their gain by Rf/Ri. DC offset errors are reduced by calculating Ri+ as Rf // Ri. In the time domain, we just calculate t as Rf . Cf.
Even the utmost mathematical areas of filter theory and spectral transforms, can be approached and solved with finite mathematics only. Both in analog and in digital electronics. After all, microprocessors are finite machines and all their calculations rely on nothing but finite mathematics and algoritms.
Stick to reality. Dont put god in your circuit.
dr.Godfried-Willem Raes
This article is part of a research project on Experimental Legacy financed by the Orpheus Institute in Ghent.
Last update: April 27th 2015
www.orpheusinstituut.be
to home page Godfried-Willem Raes