Prof.dr.Godfried-Willem RAES
Kursus: Boekdeel 4B: Akoestiek
Associatie Universiteit Gent : School of Arts
| <Terug naar inhoudstafel kursus> | leskalender |
4500:
Inleiding tot de Akoestiek
Algemene Inhoudsomschrijving
In deze hoofdstukken wordt gepoogd musici, komponisten, producers en instrumentenbouwers in spe een minimale natuurwetenschappelijke basis te geven met betrekking tot datgene waar zij zich objektief mee bezighouden: het (georganiseerd) produceren van klanken en geluiden. Daarbij komen zowel de wetmatigheden die ten grondslag liggen aan de werking van allerhande muziekspeeltuigen als de wijze waarop hun klanken en geluiden worden overgedragen uitvoerig aan de orde. Tevens willen we pogen hen daarbij ook vertrouwd te maken met meettechnieken evenals met instrumenten en toestellen die hen zeer waarschijnlijk zowat overal zullen omringen en in funktie waarvan aan hen ook bepaalde eisen zullen worden gesteld: geluidsversterking, opname, korrektie, synteze... Een zekere kennis van deze technologien lijkt meer dan ooit onontbeerlijk om als professioneel muzikus en/of komponist-producer en/of instrumentbouwer binnen de huidige maatschappij optimaal te kunnen funktioneren.
Muziek is een bijzonder aards verschijnsel: planeet aarde bestaat uit een vloeibare kern en een harde korst eromheen. Bovenop die korst bevinden zich vloeistoffen (de zeeen), organische substanties (leven) en daarbuiten een dampkring. De aarde -een geoide, een wat afgeplatte bol, draait om haar as en bovendien in een ellipsvormige baan, omheen de zon. Verder draait er nog een maan rond deze aarde. Deze hele konstellatie heeft nogal wat gevolgen voor de eigenschappen van geluid en trillingsverschijnselen op die aarde.
De dichtheid van de dampkring is verschillend naargelang de plaats op aarde en naargelang de afstand van de aardkorst. Bovendien is die dampkring doorlopend in beweging en is de samenstelling ervan allesbehalve konstant.
Akoestische basis
Het is uitermate belangrijk te beseffen dat tussen fysisch en perceptorisch geen noodzakelijk een-eenduidig verband bestaat! Als musici leggen wij uiteraard de nadruk op de perceptorische eigenschappen van het geluid. Deze zijn echter steeds het gevolg van een bepaalde wisselwerking tussen fysische stimuli en intrinsieke eigenschappen van het perceptieapparaat ( het oor) en de daaraan gekoppelde cerebrale en neurologische verwerking der ontvangen prikkels. Het menselijk oor is meer dan alleen maar een waarnemingsmechanisme. Het is tevens informatieverwerkend. Deze eigenschap alleen reeds maakt dat we een mikrofoon niet kunnen omschrijven als een substituut voor het oor. Auditieve waarnemingen die niet gekorreleerd zijn aan trillingen van luchtmolekulen (oorsuizen, hoge fluittonen...) behoren niet tot het domein van de fysika maar wel tot dat van de audiologie, een onderdeel van de medische wetenschappen. De wetenschappelijke studie van de geluidsperceptie heet de psychoakoestiek en is een onderdeel van de waarnemingspsychologie. De manier waarop wij muziek horen, verwerken en ervaren wordt dan weer bestudeerd in de kognitieve muzikologie.
Lucht is het medium waarin het geluidsfenomeen zich in onze dampkring hoofzakelijk afspeelt.
Lucht is een mengsel van verschillende gassen, dampen en stofdeeltjes.
Droge en gefilterde lucht bestaat uit volgende gassen:
| gassoort | volume deel | molekulair gewicht | gaskonstante |
| zuurstof | 0.2090 | 32.00 | 6.688 |
| stikstof | 0.7813 | 28.02 | 21.892 |
| argon | 0.0094 | 39.90 | 0.375 |
| koolzuur | 0.0003 | 44.00 | 0.013 |
| LUCHT: | 1 | 28.968 |
De molekulen van de gassen waaruit lucht bestaat bewegen kriskras met snelheden van 450 tot 500 m/s (bij 20 graden Celsius en normale atmosferische druk) in alle richtingen. De gemiddelde vrije weg tussen die molekulen onderling is 0.06µm (6E-8 m). Het gemiddeld aantal molekulaire botsingen per sekonde is dan ook: fm= 500 m/s / 6E-8 = 10GHz. Dit is wat bedoeld wordt wanneer we het over de thermische agitatie van de molekulen hebben.
De verzamelde lucht die door de zwaartekracht rond onze planeet aanwezig is noemen we de dampkring. De beweging van die lucht onder invloed van de aardrotatie enerzijds en de verwarming door de zon anderzijds, noemen we wind. De dampkring wordt ijler naarmate we ons van het aardoppervlak verwijderen. De luchtdruk neemt af en ook de samenstelling van de dampkring verandert, niet in het minst omdat er boven de wolken minder waterdamp in de lucht aanwezig is.
Enkele belangrijke fysische eigenschappen van geluid:
- voortplantingssnelheid van het geluid in een gasmengsel:
Eerste vereenvoudigde benadering:
in komputer-Basic notatie: v = ((1.4 * P) ^ ( 1/2 )) / d
waarin:
Deze voortplantingssnelheid kan ook uitgedrukt worden in funktie van de temperatuur:
waarin T= temperatuur in graad Celsius. Merk op dat
De geluidssnelheid in droge lucht bij 0 Celsius is 331.45 m/s, bij 16 graden 340 m/s, bij 20 graden 343 m/s.
In traditionele notatie:
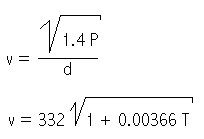
De geluidssnelheid in een gas en in lucht is recht evenredig met de vierkantswortel uit de absolute temperatuur. Een van de voor musici nogal belangrijke konsekwenties hiervan is dat de stemming van instrumenten die van een trillende luchtkolom gebruik maken ( blaasinstrumenten & labiaalpijpen in het orgel) afhankelijk is van de temperatuur. De la wordt hoger naarmate het in de koncertzaal warmer wordt. Dit is echter niet op dezelfde wijze het geval voor andere instrumenten (snaren , gestemd slagwerk), zodat ruimere afwijkingen in temperatuur steeds een onstembaar orkest zullen opleveren. Een duo voor klarinet en vibrafoon of marimba bij 30 graden Celsius kan onmogelijk nog juist gestemd worden. Bij 10 graden overigens evenmin. Daarom werd de standaard diapason La = 440 Hz ook bepaald bij een vastgestelde temperatuur (16 graden Celsius). (1939, internationale konferentie over de Standaard toonhoogte in London).
[de geluidssnelheid in stoom bij 100 graden is 404.8 m/s, waardoor het stijgend glissando van een waterketel die aan het koken wordt gebracht kan worden verklaard. De geluidssnelheid in heliumgas -gebruikt o.m. bij het duiken, ter vervanging van stikstof- is 970 m/s. Wanneer we dit gas in onze longen hebben, klinkt onze stem zowat een oktaaf hoger, vandaar de Donald Duck stem die we dan verkrijgen].
Meer exakte benadering:
Uit empirisch wetenschappelijk onderzoek is gebleken, dat de voortplantingssnelheid van een trilling door een isotropisch medium mede afhankelijk is van de frekwentie, wat te wijten is aan de dispersie. In vaste stoffen is de variatie van de voortplantingssnelheid in funktie van de frekwentie kleiner dan 1%, in vloeistoffen < 25%, maar in gassen kan de afwijking nog veel grotere waarden aannemen en wordt ze zelfs extreem wanneer de golflengte van het geluid kleiner is dan de vrije weg tussen de afzonderlijke gasmolekulen. Dit is het geval rond 1MHz, of voor golflengtes van ca. 0.3mm. De voortplantingssnelheid neemt steeds wat af met toenemende frekwentie. De formule komt er dan eerder uit te zien als v = SQR(1.4*P)/( d * (f^k)), waarin f de frekwentie en k een exponent in funktie van de dispersie. Voor trillingen binnen het audiogebied zijn de afwijkingen niet spektakulair maar niettemin meetbaar en ook hoorbaar. Zij zijn een van de elementen waarmee de inharmoniciteit van trillende luchtkolommen kan worden verklaard.
cfr. Avad Behari Bhatia, 'Ultrasonic Absorption', 1985, (1967)
- Golflengte van een periodieke geluidstrilling
Waarin l = golflengte in meter (hiervoor wordt meestal de griekse letter lambda gebruikt).
Een toon van 20 Hz komt overeen met een golflengte van 17meter. Een toon van 20kHz heeft een golflengte van slechts 17mm. Het eenvoudige feit dat de afmetingen van muziekinstrumenten toenemen naarmate hun tessituurbereik lager begint, staat hiermee in verband.
- Intensiteit van een geluid in funktie van de afstand
De voortplanting van een geluidsgolf moet in de meeste gevallen worden beschouwd als sferisch ( bolvorming) vanaf de bron. Dit gaat op voor alle gevallen waarbij de bron van het geluid kleiner is dan de golflengte van het voortgebrachte geluid. De geluidssterkte nu, is afhankelijk van de afstand tot de bron en wel alsvolgt :
Het is belangrijk in het hoofd te houden dat de geluidssterkte afneemt met het kwadraat van de afstand! Onthoudt dat r als een kwadraat in de noemer staat van de formule. Die noemer is trouwens niet anders dan de oppervlakte van een bol. Wanneer dus een geluid waargenomen op 1 meter afstand van een bron een bepaalde sterkte heeft, dan bedraagt die sterkte op 2 meter afstand nog slechts een kwart, op 4 meter , een zestiende...enz. Merk ook op dat de formule tot absurditeiten aanleiding geeft wanneer we r zouden laten naderen tot nul... het lijkt er dan immers op dat onafhankelijk van het vermogen de geluidsdruk onbeperkt tot oneindig groot zou moeten toenemen. Dat is echter slechts een paradox, want er kan fysisch slechts een geluidsdruk opgebouwd worden op een minimale afstand van de geluidsbron. Meestal (voor periodieke golven) neemt men daarvoor een gehele periode van de laagste frekwentie waarvoor men wil meten. Bovendien geldt ook hier de wet van behoud van energie, waardoor het akoestisch vermogen nooit groter kan zijn dan de energie van zijn oorzaak, de mechanische arbeid nodig voor de excitatie.
Een groot symfonisch orkest (75 man sterk) vertegenwoordigt een akoestisch potentieel vermogen bij de bron van circa 100 Watt, of 140dB. (ref. 10 pW/m2) Fluisteren levert daareentegen een akoestisch vermogen op van slechts 1 nanoWatt! Het afschieten van de Saturnus draagraket gaat gepaard met een akoestisch ontwikkeld vermogen van 50 tot 100 MegaWatt (200dB, ref. 10pW)...
Wil je deze vermogens omrekenen naar de in akoestiek gebruikelijke geluidsdrukken, dan kan je volgende eenvoudige formule gebruiken:
Lp = 20 log p + 94
Hiermee kan je de referentiewaarden voor vermogen (10 pW/m2) omzetten in dB's met referentiewaarde van 20 microPascal. In de formule staat p voor het akoestisch vermogen, uitgedrukt in Watt. De 94 is uitgedrukt in dB en is de omzettingskonstante waarmee de beide referenties aan elkaar zijn gerelateerd.
Het hiervoor vermelde symfonisch orkest produceert dan een geluidsdruk van Lp = 20( log 100) + 94 = (20 * 2) + 94 = 132 dB. Een potentieel erg gevaarlijke machine dus, waarvan onlangs trouwens onomstotelijk werd bewezen dat de leden er permanente gehoorschade aan overhouden...
Ter orientatie en om wat vertrouwd te worden met de grootheidsorden, hierbij volgende tabel:
| Akoestisch vermogen | dB (met ref. 10 pW) | Geluidsdruk in dB (ref 20 microPascal) | beschrijving soort geluid |
| 100.000.000 | 200 | +250dB | Saturnusraket |
| 10.000 | 160 | +174dB | Starten Boeing 707 |
| 100 | 140 | +132dB | Symfonieorkest |
| 1 | 120 | +94dB | Kettingzaag |
| 0.01 | 100 | +54dB | motor gewone auto |
| 0,0001-0,00001 | 80-60 | +14dB tot -6dB | normale stem |
| 0,000.000.01 - 0,000.000.001 | 40-20 | -66dB tot -86dB | fluisteren |
| 0,000.000.000.001 | 0 | -94dB | gehoorgrens |
Noteer dat de totale geluidsdruk voor een bolvormige straler p(r) = I / r, waardoor de indruk zou kunnen ontstaan dat de druk lineair afneemt met de afstand! In deze formule wordt evenwel slechts de totale effektieve geluidsdruk weergegeven, niet die zoals die ooit door enige waarnemer -die zich immers op een bepaalbaar punt bevindt- zou kunnen worden waargenomen.
De waargenomen geluidsdruk van een straler hangt mede af van de ruimte vanwaaruit onze bol-straler straalt. Deze afhankelijkheid wordt uitgedrukt middels de richtingsfaktor (directivity factor) Q.
We onderscheiden volgende gevallen:
1. Ruimtestraler (hierbij zijn er geen begrenzingen) Q = 1
2. Halve ruimte straler (de straler is begrensd door een enkel 'oneindig' vlak: Q= 2
3. Kwartruimte straler (de straler is begrensd door twee 'oneindige' vlakken - een tweevlakshoek dus) : Q= 4
4. Achtsteruimte straler (de straler is begrensd door drie 'oneindige' vlakken -een ruimtehoek dus): Q = 8
5. Tetraedrische straler (de straler is begrensd door die 'oneindige' vlakken onder een hoek van 60 graden: Q = 12
Q is de faktor waarmee we de geluidsdruk op een punt bij de bron mogen vermenigvuldigen, wanneer aan de ervoor geldende voorwaarden voldaan is. (Wanneer we het over het totaal akoestisch vermogen hebben, moeten we de wortel nemen uit deze Q faktoren. Bij een halve ruimte straler verdubbelt het vermogen en neemt het dus toe met maximaal 3dB)
In alle praktische omstandigheden zal de geluidsdruk steeds lager uitvallen dan de op grond van vorige formules berekende waarden. De viscositeit van lucht vormt immers een dempende faktor evenzeer als water en stofdeeltjes in de lucht geluid absorberen; voorts, obstakels, het niet aan het wiskundig vlak voldoen van de begrenzende oppervlakte, wind en thermische bewegingen van de lucht... (Mist, dat is waterdamp, levert een geluidsverzwakking op van ongeveer 6db per 300 meter).
Geluid en elektromagnetisme:
Het frekwentiegebied dat we meestal beschouwen als we het over geluid hebben heeft een tegenhanger in het gebied van het elektromagnetisme. Dit wil zeggen dat die frekwenties, wanneer ze een elektrische stroom karakteriseren, meteen ook als elektromagnetische straling kunnen voorkomen. Net zoals van die elektrische stroom, is de propagatiesnelheid van die elektromagnetische golven nagenoeg de lichtsnelheid. Een door een mikrofoon in een elektrische stroom omgezet geluidssignaal, volgt de wetten van de elektriciteit en het elektromagnetisme. In een luidspreker wordt het elektrisch signaal opnieuw omgezet in trillingen van luchtmolekulen. Van dan af, gelden de wetten met betrekking tot propagatie van geluid. Het is perfekt mogelijk geluid, eens omgezet in een elektrisch signaal, langs elektromagnetische weg uit te zenden en vervolgens weer te ontvangen. Het volstaat de luidspreker te vervangen door een geschikte spoel, uitgevoerd als raamantenne of als stroomlus. Het spreekt echter vanzelf dat we deze elektromagnetische straling niet met onze zintuigen kunnen waarnemen.
Overzicht van elektromagnetische golven en frekwenties.
maar niet zonder een heel klein beetje wiskunde ...
De decibell, zoals hiervoor reeds argeloos geintroduceerd, is geen eenheid zoals de meeste andere fysische grootheden. Het is bij mensen die niet beroepshalve met wetenschap en technologie bezig zijn, een van de meest misbegrepen begrippen uit de wetenschap in het algemeen. De decibell is immers een maat voor een verhouding van twee grootheden tegenover elkaar. Deze maat kan in zowat alle bereiken van de wetenschap worden gebruikt om de meest diverse grootheden te vergelijken. Ze wordt echter vooral daar gebruikt waar de verhoudingen tussen de getallen erg groot zijn. De bewerkingen worden er aanzienlijk door vereenvoudigd. De wiskundige basis ervan is de logaritme. De logaritme van een getal is bij definitie niets anders dan de exponent waartoe we een bepaald grondtal moeten verheffen om dat getal te bekomen. Dus :
Als grondtal voor de berekening van logaritmen komen het getal 10, het getal 2, en het irrationaal getal e het meest voor. Voor het begrip van het wezen van decibells als grootheid spelen alleen de logaritmen met grondtal 10 een rol. Wanneer we 'log' in een formule zien staan, is hier steeds de logaritme met grondtal 10 bedoeld. De definitie van logaritmen met grondtal 10 wordt dan ook:
Het zal duidelijk zijn dat wanneer x kleiner is dan 1, de logaritme van x , negatief wordt. Is x = 0 dan is de logaritme van x oneindig klein. Overigens is dit een 'ongeldige bewerking' , analoog aan delen door 0. Ga zelf na dat volgende waarden juist zijn:
log 0.01 = -2 log 0.1 = -1 log 1 = 0log 10 = 1log 100 = 2log 1000 = 3...log 1.000.000.000= 9Merk op dat het tientallig logaritme van veelvouden van 10 zelf eenvoudigweg overeenkomt met het aantal nullen in het getal. Bij getallen kleiner dan 1, met het aantal nullen na de komma vermeerderd met 1.
Verifieer ook dat het optellen van logaritmen overeenkomt met het uitvoeren van een vermenigvuldiging:
log 10 + log 100 = 310 * 100 = 1000log 1000 = 3De decibell nu , is eigenlijk het tiende of twintigste deel van de alsdusdanig nooit gebruikte Bell. We delen door twintig wanneer we te maken hebben met grootheden in 1 enkele dimensie: krachten, spanning, stroom, geluidsdruk... en door tien wanneer het gaat om grootheden met 2 dimensies: vermogen, energie, ... Het onderscheid werd ingevoerd om de rekenkunde met dB te vereenvoudigen en ook konsistent te houden ook wanneer diverse parameters (of dimensies) in het spel zijn.
Dus 10 dB = 1 Bell, of, 1 dB= 1 Bell / 10 of 1 Bel l/ 20
De Bell nu (genoemd naar Alexander Graham Bell) werd gedefinieerd - maar nooit gebruikt als eenheid- alsvolgt :
In woorden uitgedrukt is het dus het logaritme van de verhouding tussen twee grootheden uitgedrukt in eenzelfde eenhedenstelsel.
De standaard definitie van de decibell wordt dus :
Wanneer het evenwel om spanningen of andere 1-dimensionele grootheden gaat, i.p.v. om vermogensverhoudingen, wordt dit :
De decibell heeft slechts dan betekenis wanneer we weten welke referentiewaarde gebruikt wordt voor de vaste grootheid in de verhouding G2/G1. In de audio-elektronika zijn hiervoor bepaalde standaardreferenties vastgesteld :
in termen van elektrische spanning noteren we :
Geluidsdruk wordt eveneens in decibell uitgedrukt , en hiervoor geldt als referentie dat :
SPL staat hier voor Sound Pressure Level, of geluidsdrukniveau.
De beruchte waarde van 120 decibell geluidsdruk komt dan ook overeen met een absolute geluidsdruk van 20 Pascal. Deze waarde is berucht omdat zij met de pijngrens overeenkomt. Het zal duidelijk zijn dat een sterkteverhouding van 1 op 1.000.000 in decibel numeriek wordt teruggebracht tot een verhouding van 0 tot 120, wat het rekenen aanzienlijk eenvoudiger kan maken. Een verschil van 6dB komt steeds overeen met een grootheidsverhouding van 1 op 2, dus halvering bij -6dB, verdubbeling bij +6dB. We zullen verder zien dat bij het uitdrukken van de gevoeligheid van mikrofoons, heel vaak uitgegaan wordt van 94dBspl, wat overeenkomt met een geluidsdruk van 1 Pascal.
Ook voor het akoestisch vermogen (Akoestische Watt) bestaat een referentie voor de omzetting naar decibells :
(Noteer: 1 picowatt = 0.000 000 000 001 Watt).
Voorts wordt de decibell ook nog gebruikt voor het tot uitdrukking brengen van signaal/ruisverhoudingen in komponenten van geluidsinstallaties, bij radiozenders..., voor het uitdrukken van versterkingsfaktoren in audioversterkers, mixers, antennes,... , voor het uitdrukken van door netwerken geintroduceerde signaalverzwakkingen in filters, modulatieapparatuur..., voor de verstaanbaarheid van sprekers in lawaaierige omgevingen... Kortom, de decibell wordt zowat overal in de hedendaagse techniek aangewend. We kunnen er echt niet omheen.
dB in de audiotechnologie...
Een ander gebruik van de dB in de elektronika en de audiotechnologie ontmoetten we steevast wanneer signaal/ruisverhoudingen van audioinstallaties of elektronische schakelingen moeten worden tot uitdrukking gebracht. Bij analoge schakelingen en installaties geldt daarvoor de dBV referentie ( 0dB= 600mW in een 600 Ohm belasting, of 0.775mV), maar vanzodra we te maken krijgen met signalen in het digitale domein onstaat er een intrinsieke relatie tussen enerzijds het oplossend vermogen (in bits) en de haalbare dynamiek (in dB) anderzijds. Zo laat een 16-bit DAC (Digitaal-analoog konvertor) een dynamiek zien van maximaal 96dB, wat we dan moeten interpreteren als de verhouding van het kleinste nog oplosbaar (in een unieke kode omzetbaar) signaal tot het grootste. Het komt eenvoudigweg overeen met de grootste numerieke getalwaarde die met 16 bits kan worden geschreven tegenover de kleinste waarde (steeds 1 in dit geval).
Volgende kleine tabel laat het verband eenvoudig inzien:
16 bit = 96dB15 bit = 90dB14 bit = 84 dB13 bit = 78 dB12 bit = 72 dB11 bit = 66 dB10 bit = 60 dB9 bit = 54 dB8 bit = 48 dB7 bit = 42 dB6 bit = 36 dB5 bit = 30 dB4 bit = 24 dB3 bit = 18 dB2 bit = 12 dB1 bit = 6 dBWanneer we res de resolutie noemen van een DAC
of ADC (uitgedrukt in aantal bits) dan kunnen we dit ook in een eenvoudige
formule uitdrukken alsvolgt:Dynamiek = (20 * Ln(2^res))/Ln(10)
= 20 * LOG(2^res)De dynamiek volgt nu in dB's.Het omgekeerde, nodig wanneer we willen weten met
welke hoogste numerieke waarde een bepaalde dynamiek gegeven in dB overeenstemt
volgt uit volgende formule:Maxval = EXP((Dynamiek * (LOG(10)/20))
= EXP (Dynamiek * 0.1151293)Eenheden uit de fysika, gebruikelijk in de akoestiek:
Druk:
uitgedrukt in Pascal, afgekort als Pa
1 Pascal = 1 N/m2 = 0.01mbar = 1 kg/m.s2
10bar = 1MPa = 1N/mm2
1 mBar = 100Pa
1mBar = 10mm waterkolom of 10mm H2O (een eenheid gebruikelijk in de orgelbouw)
1 Bar komt overeen met de normale gemiddelde luchtdruk ter hoogte van de zeespiegel op aarde. In Pascal is dit dus 100.000 Pa of 100kPa
Omdat ondanks internationale afspraken terzake, men in ekonomische en technische middens ook vandaag nog vaak druk aantreft uitgedrukt in de meest diverse anakronistische eenheden, geven we hier een omzettingstabelletje. De tabel kan ook nuttig zijn bij het doornemen van historische literatuur m.b.t. akoestiek en instrumentenbouw.
PSI inch H20 inch Hg kPa mBar cm H20 mm Hg mBar 0.01450 0.40147 0.02953 0.10000 1.0000 1.01973 0.75006 cm H20 1.42237E-2 0.3937 2.8958E-2 0.09806 0.9806 1.000 0.7355 mm Hg 1.9337E-2 0.53525 3.9370E-2 0.13332 1.3332 1.3595 1.0000 kPa 0.14504 4.00147 0.2953 1.0000 10.000 10.1973 7.5006 inch Hg 0.4912 13.596 1.0000 3.3864 33.864 34.532 25.400 inch H20 3.6127E2 1.0000 7.3554E2 0.2491 2.491 2.5400 1.8683 PSI 1.0000 27.680 2.036 6.8947 68.947 70.308 51.715 PSI (pounds per square inch!) vinden we vaak terug op luchtbanden van fietsen en autos en op manometers van gasflessen. mmHg en inch Hg (de hoogte van een vertikale kolom gevuld met kwik) treffen we aan op oude europese, resp. angelsaksische, barometers. cm H20 of inch H20 (de hoogte van een vertikale waterkolom) op vele ventilatoren en ook (in mm dan) op blazers voor orgels (radiale kompressoren).
Nota bij de tabel:
Kracht:
uitgedrukt in Newton, afgekort als N
1 Newton = 1 kgm/s2 = 1 J/m
Definitie:
Een kracht van 1 Newton geeft aan een massa van 1 kg in 1 sekonde een snelheidsverandering van 1 m/s.
Massa:
uitgedrukt in kg. De massa van een stof hangt samen met het atoomgetal van de samenstellende atomen van die stof en uiteraard met de hoeveelheid ervan. De soortelijke massa (kg/m^3) is per definitie onafhankelijk van de hoeveelheid. Wanneer het gaat om voorwerpen waarvan in hoofdzaak de lengte belangrijk is (bvb. snaren), kan de soortelijke massa ook uitgedrukt worden in kg/m en voor vlakke voorwerpen (membranen) in kg/m^2.
Gewicht:
uitgedrukt in Newton
eigenlijk is dit de kracht die op een massa werkt. De oorsprong van die kracht (op aarde) is de zwaartekracht. Wanneer die kracht wegvalt is de massa gewichtloos.
G = m.g, waarin m = massa (in kg) en g = 9.81 m/s2 (valversnelling op aarde)
Energie:
uitgedrukt in Joule, afgekort als J
1 Joule = 1Nm = 1 Ws = 1 kgm2/s2
Elektrische energie wordt meestal uitgedrukt in kWh. 1 kWh = 3.6MJ
Vermogen:
uitgedrukt in Watt, afgekort als W
1 Watt = 1 J/s = 1 Nm/s = 1 VA = 1 m2kg/s3
Frekwentie:
uitgedrukt in Hertz , afgekort als Hz. Wordt alleen gebruikt voor periodieke verschijnselen en distributies.
1 Hz = 1/s
veelvouden: kHz , MHz, GHz, THz (telkens een faktor 1000 groter)
Tijd:
uitgedrukt in sekonden. (s). De periodetijd van periodieke verschijnselen is het omgekeerde van hun frekwentie: T = 1 / f
veelvouden: minuten, uren, dagen, maanden, jaren (dit zijn geen fysische eenheden)
deelfaktoren: ms, µs, ns, ps, fs (telkens een faktor 1000 kleiner)
Impedantie:
uitgedrukt in Ohm
1 Ohm = 1 V / A
Faze:
uitgedrukt als een hoek in graden (een cirkel = 360°) of -bij voorkeur- in radialen (een cirkel = 2 ¶ radialen).
Temperatuur:
uitgedrukt in Kelvin, afgekort als K
0 K = -273.15° Celsius, dit is het absolute nulpunt.
Filedate: 840928/951102/ 2013-10-28
| Terug naar inhoudstafel kursus: <Index Kursus> | Naar homepage dr.Godfried-Willem RAES |